61 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Q ka root iota hai kya?
no
nahi hai
hmmm
What is the ans?
lemme share
you stormy long time no see
Hopped on cuz it’s a new year loll
answer is 5
Alr
so you are going to reverse engineer the question ?
Trying to do that lol
I did polynomials last year yk so a bit rusty
they are teaching me polynomials in functions chapter right now in class 12th
Oh so u also learnt it last year
Excuse me for my new year jokes I have to abuse it today
Doable by complex.
Like the roots of the second polynomial are 5-th roots of 1.
Then by remainder theorem plug in to get 5.
Is that the answer?
Yes
OHHH YEAHH
i forgor
man complex number showing up legit anywhere
Q(x) pe GP ka formula laga de
Algebra ka undertaker fr
what, can u explain this
Let $P(x)=Q(x) \cdot f(x)+r(x)$
Plug in $x=e^{\frac{2ni \pi}{5}}$
SirLancelotDuLac
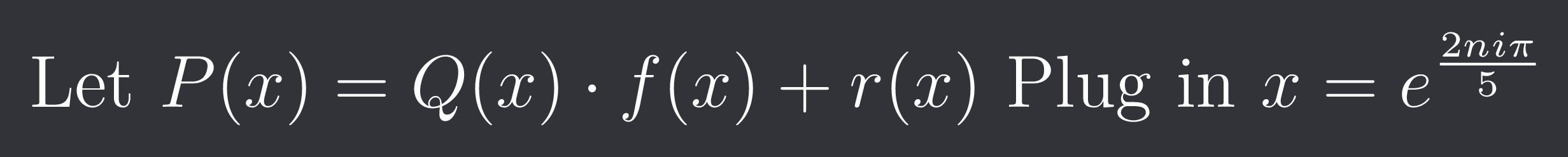
For all these values r(x)=5. Hence the remainder is indeed 5.
What if the remainder is not five for each case?
(Kinda obvious point but I used to miss it: r(x) must be a cubic which acquires value 5 at 4 points, so yeah)
Then form the cubic and painstakingly find coeffecients ig.
Or maybe some other method will have to try.
Could we derive a general form for P($x^{n}$})modP(x)?
Opt
Compile Error! Click the :errors: reaction for more information.
(You may edit your message to recompile.)

Ah just figured a nice counter to that.
We can't find a root of higher level polynomial.
Ah nvm that argument is wrong tho...
Ig it is not possible but so the approach should be to prove that its not possible and I don't have many ideas for that. :sweaty:
Understandable
Maybe we could use the fact that the formulae for roots of quintic/higher polynomials doesn't exist and somehow reach contradiction.
But don't see a simple proof for the same.
Galois Theory fr fr
huh
I am confused lol
the answer is 5 though
?
Qx pe GP ka formula laga ke
x⁵=1 ke roots
complex wale jo rahenge
unko Px pe put kar
qx pe gp ka formula ?
geometric progression bol rhe ho ?
so sum of terms gp se
$x^5-1/$x-1
Abhi
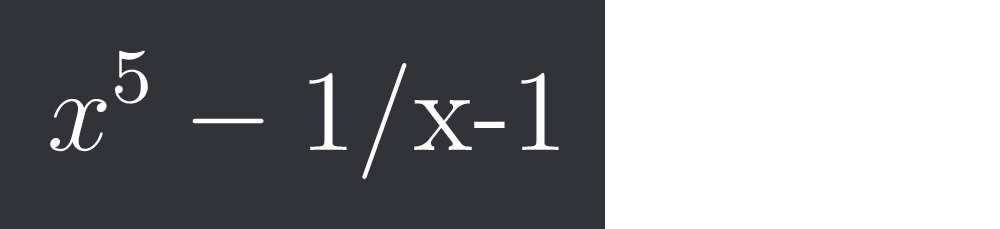
ye aa rha hai
@Dexter bhai help karde dimaag bilkul bhi nhi chal rha
yo @Opt can you help ?
Yeah that.
:pepestare:
please solve the ques somehow
I can't solve it still
:moc_champ_sad:
Lancelot gave you the solution right?
With complex numbers.
no then
he said it was wrong
.
this
maybe I am confused
That's not related at all
Solution ended here
Rest was pointless conversation
Yeah that was for something else 😅.
oh I have to try it
my brain is fogged today
literally can't do shit today
yes
no x⁵=1 and x=/1
now**
to complex roots nikaal le
so x=1 aa gya
to complex roots ?
no
X=1 not valid na
GP ka sum
complex 2 nahi padha hai na tune?
Allen mein h kya?
denominator infinite
haa
yeah to complex numbers last chapter hai 12th ka tere liye
accha
mereko lga
usse ez hoga ye sawaal
allen ne padha diya
aur
merese nhi ho rha
Polynomial ka bhi koi tareeka hoga tbh
but idk that
i do all the questions of quadratic and polynomial from complex numbers now
😭
its easier that way
ek concept se saare sawaal bante hai
hmm
@Opt you know any other method than the complex one
?
We are not taught complex no sadly
Well you don't need to know complex tbh.
The equation you have is $\frac{x^{5}-1}{x-1}=0$ (x is not 1.). So $x^{5}=1$ for all roots. Now just plug it in and then viola.
SirLancelotDuLac

Baaki remainder theorem toh you know. So the remainder polynomial is some cubic which acquires the value 5 at 4 places (at the four roots). So it is an identity and hence the remainder is 5.
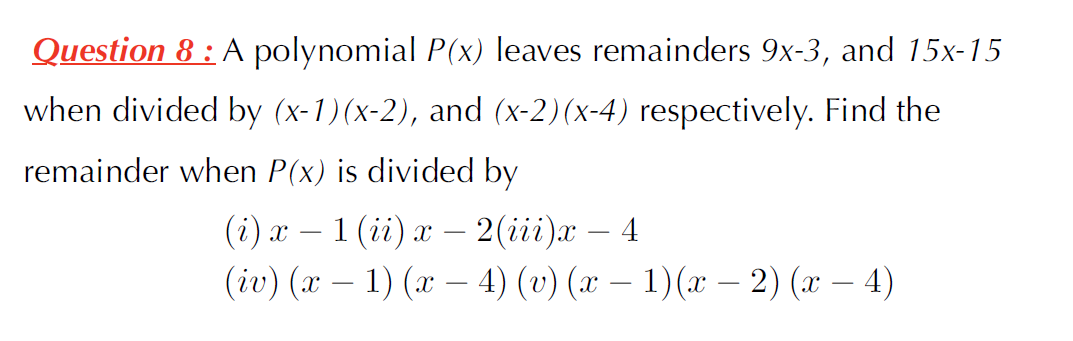
yo @SirLancelotDuLac if you are free
can you tell how to this the approach
quadratic se divide kiya hai and linear remainder hai
yup
ban gya tha mere se sir
aaj
kal brain fog
tha
aaj so ke utha
to ban gya
:kekGiggle:
matlab p(x) must be a cubic
goated
sahi hai
+solved @Dexter @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@1035556259417571408> (1035556259417571408)
Time
<t:1737255708:R>
Solved by
<@1095655769376034818> (1095655769376034818), <@1075951732460376214> (1075951732460376214)
