math
I am getting a diff ans from key, but both mine and the key satisfies it but they did it in a more of a “legit method”?
So pls lmk what ans u get

26 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.1. Now let the other roots be $\alpha,\beta,\gamma$, so you have $\alpha+\beta+\gamma=-4$ and 2 other equations. So the values of alpha, beta and gamma can be found. Now the values of q and r can also be found.
2.Long divide by $x^{2}-4x+2$. Quotient would be cubic so you would have to do 4 steps, so it may be longer and calculation errors may occur.
SirLancelotDuLac

1. is using theory of roots and 2, is just something I thought.
What i did was, I took 2 and substituted it, and got an eqn and then I substituted q and r values till it satisfied, is this correct? Prob not bc the ans is 48 and I got 6
I can send there solution if u want and I’ll try ur method in a bit and see where it goes
Substituted q and r as in how will it be divided by (x-2)^2?
Like the eqn divides with x-2 whole 2, one of the values of x can be 2 such that the eqn equals to zero, so I substituted 2 and equated it to zero and got a eqn with only q and r , after that I put random values for q and r
Would this be correct?
But there would be infinite such values of q and r?
Like it's a linear equation in 2 variables. All other values may not satisfy given conditions.
it is not given that they are integers or smthing
Mhm yah😭 how do I rule them out?
so substituting won't work
They r integers acc to what they got in the ans as well, but yah that too
The above theory of equations one is a good solution imo.
Alrighty will try it out, tysm
I got it another method, I wrote it as the product of x-2 whole square and a cubic polynomial and equated the power4,3,2 x to zero and got values, thankyou so much again :]
Good.
And also could u explain ur first method on how u got alpha beta gamma is -4, sorry we didn’t do theory of eqn yet 😭
Oh sorry. Its basically the sum of roots of equations = -b/a and so on.
But that is a fifth power eqn right?
Basically for an equation $a{0}x^{n}+a{1}x^{n-1}+...$, sum of roots taken k at a time is $(-1)^{k}a{k}/a{0}$
SirLancelotDuLac
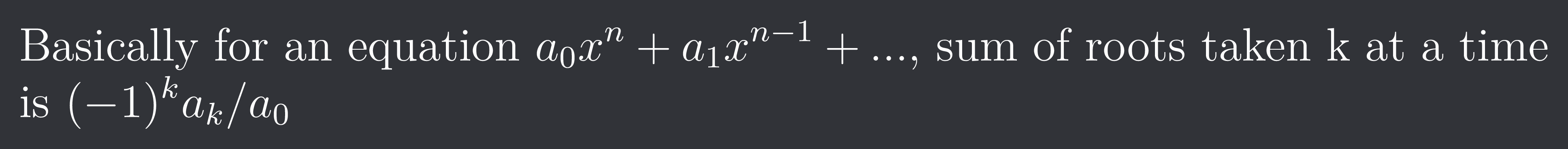
Oh ok thankyou so much :]
Sorry for the bad quality but yeah...


Got it thankyou so much again
+solved @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@821702877721657374> (821702877721657374)
Time
<t:1725722118:R>
Solved by
<@1075951732460376214> (1075951732460376214)