Circular Motion
Since w is constant, alpha = 0...so there is no tangential acceleration, only centripetal acceleration. Should we consider rotational motion about O or about O'?
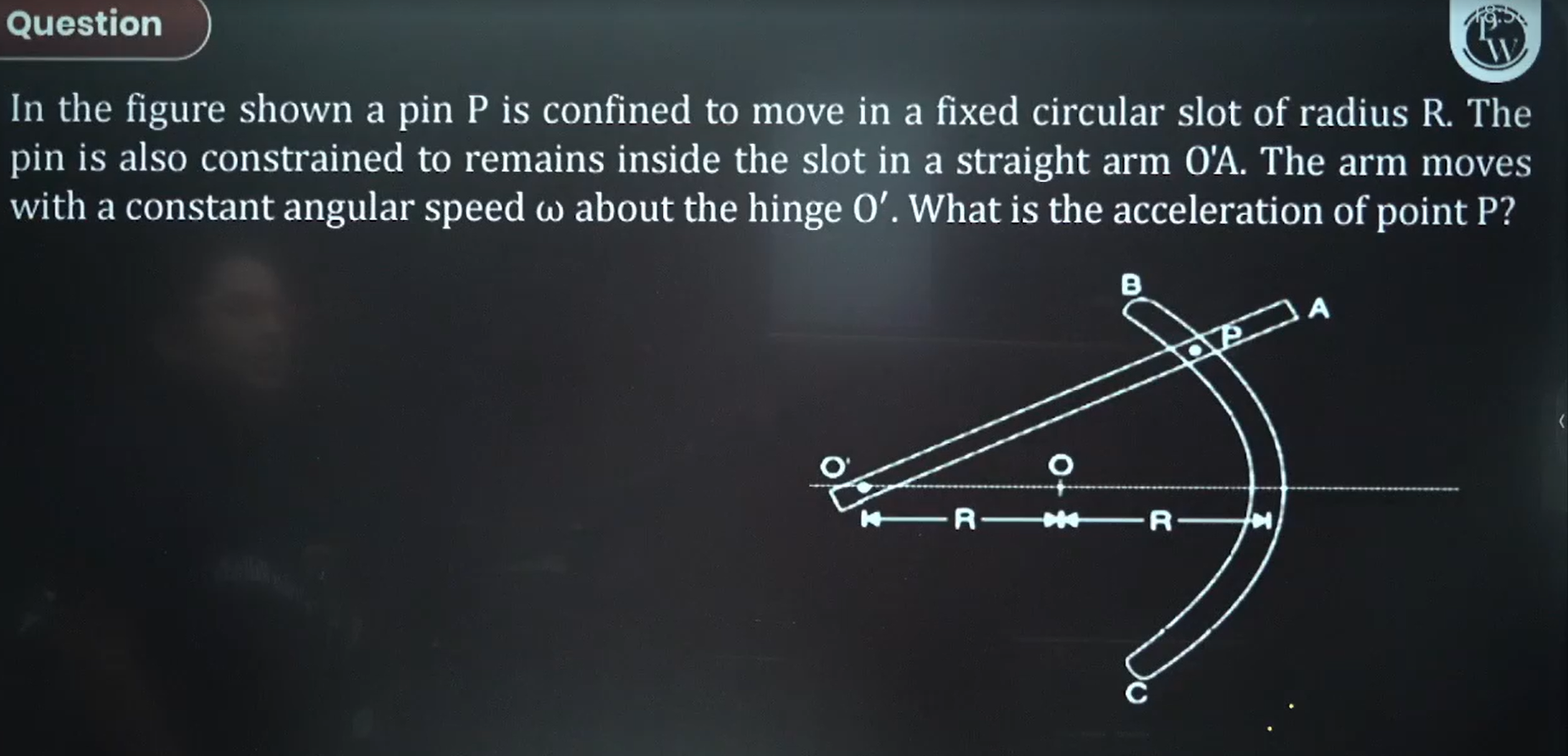
44 Replies
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.why would it be about O
idk but the answer is 4R(w)^2
if we consider it about O', I think we are supposed to get 2Rw^2
can u send what u did
This is the solution given by PW
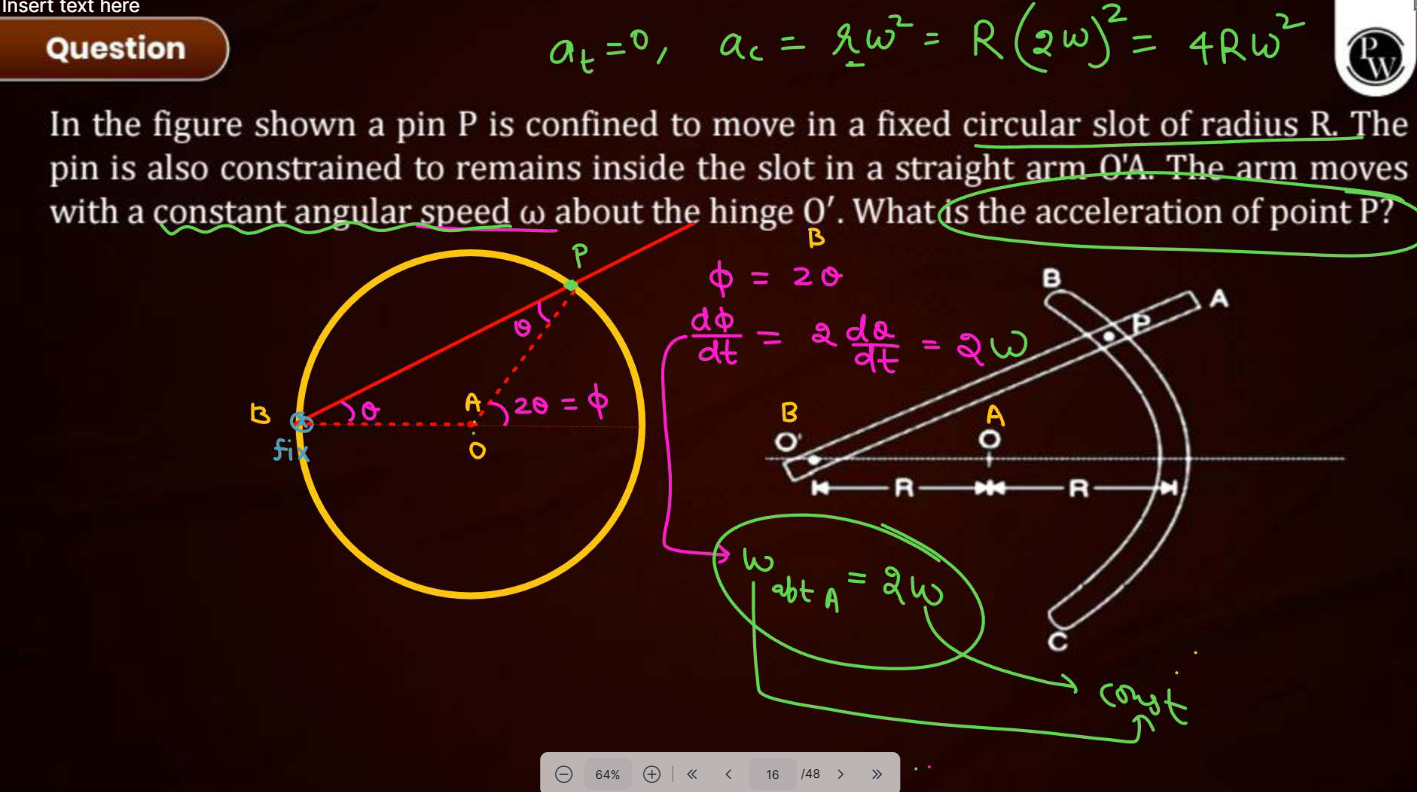
I just don't understand why they have taken centripetal acceleration wrt O instead of O'
Btw in this O is A and O' is B
ye i dont get it either ping me when someone answers
Because the pin is constrained to move about the circular armature of radius r. The other portion of the velocity is removed by the normal force from the fixed armature.
Then its just center subtends 2*(theta) if arc subtends theta at circumference property.
This explanation clears my doubts
Thanks
@Gamertug
what ? i dont understand
isnt O also fixed so isnt it also circular motion wrt to O?
Do note that the pin in this case can move along the rod (O'A), so the distance of OA' is in fact, not fixed
So it doesn't do circular motion about O'
Circular motion hence, is only about O.
it just said O' is hinge
i get why it will do circular motion about O cuz it is moving in a circle with radius R
but wont it also be about hinge
i mean ik it wont be About Hinge since it is About O , but why isnt it about Hinge
Because the pin also moves along O'A so as to move along the slot.
So the "radius about O' point" (Technically incorrect to call it radius, but anyways) keeps on changing.
Hence it is not a circular motion about O'.
well think of it this way
O' does not change position
so O'P is fixed
and P is moving
Its not tho
so why wont it be a circulat motin
why not
Okay. Consider for a moment ki the circular slot is a completely circular one. Now Let O'B be the diameter of the circular slot.
When the pin is at O' , O'P=0. Similarly when pin is at B, O'P=2R.
what
why would the pin be at O'
The rod is rotating with constant omega right? But the direction of the velocity at point P is expected to be perpendicular to O'P, which is not perpendicular to OP. So consider the component along OP and perpendicular to OP. The component along OP vanishes because of the normal force.
i cant understand the part after considering component
*Assuming the circular slot to be fully circular
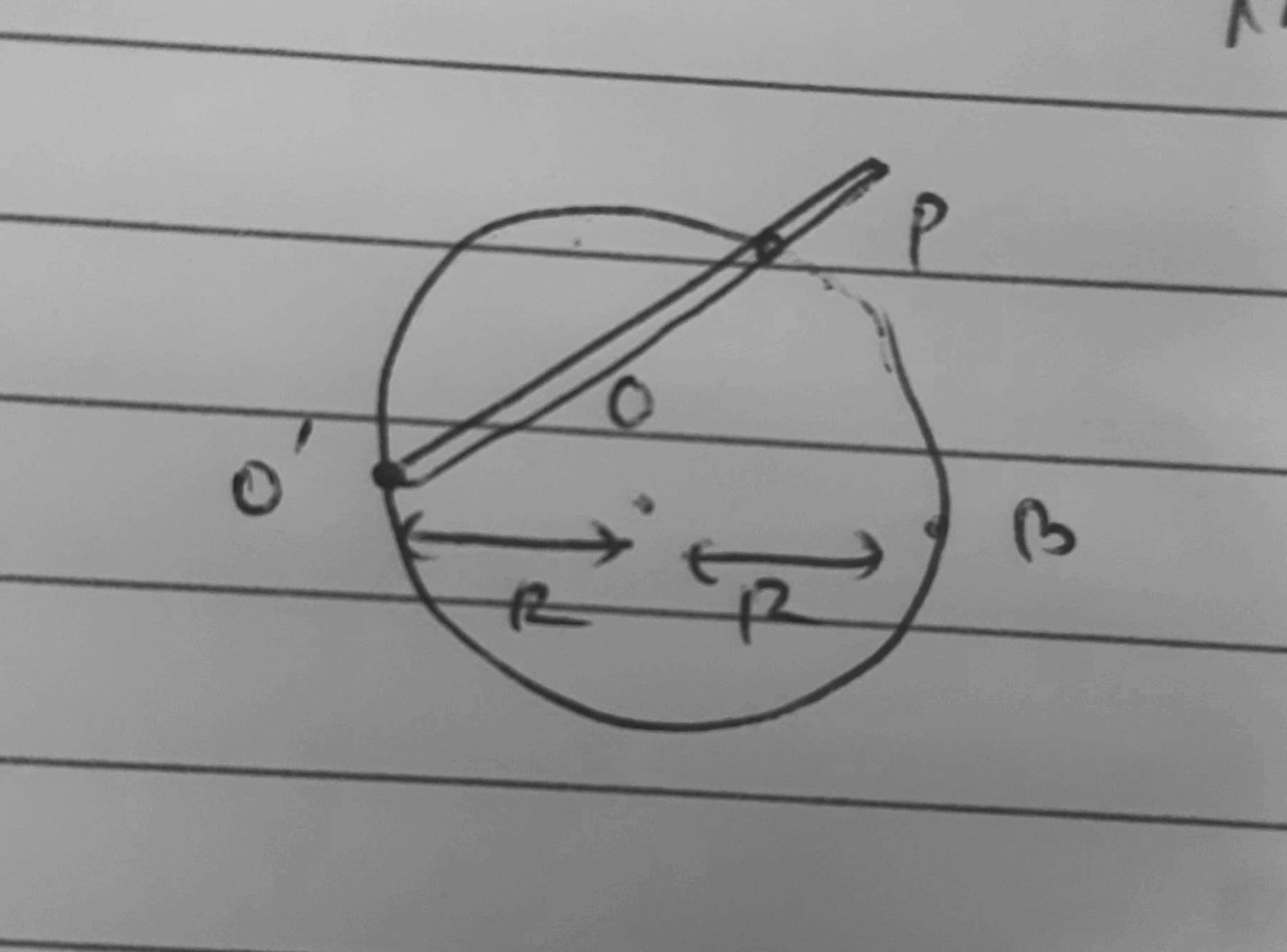
why would it be moving in complete circle
its only that part as shown in question no?
from B to C
and O'P wont be changing from B to C
It absolutely would be.
Let the angle PO'O be alpha then the value of POR is 2 alpha. So find the height of P from OO' and hence find the length OP.
i just dont get how
its a rigid rod
It will come out to be different from 2R
O'P will not be changing
But the pin can move along O'A right?
So O'P can change.
why would it , wont the slot stop it , also lets say that it does move
that means
hinge will also move
since rod is rigid
but hinge cant move
how is POR 2 aplha
Angle subtended by arc at center is twice of that at circumference.
oh ye mb
and what will that do
Find geometrically the distance O'B. It won't come out to be 2R
wait
then what is going on
hinge cant move
and point P is fixed
wth is happening then
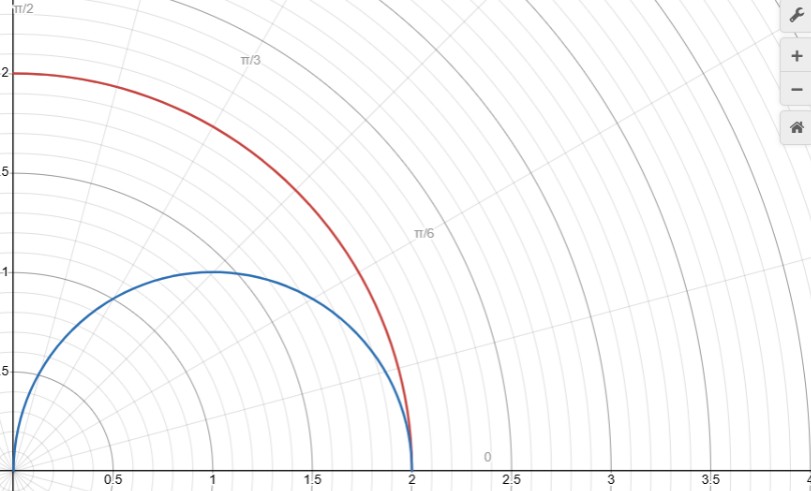
Here, blue is the locus of the pin and red is the locus of the end of the rod.
Now try to visualize a line from origin cutting both these circles at some point. Rotate this line in your mind and look at how the points move.
ok wait i understand O'B wont be 2R
but why
Hinge is fixed and P is fixed so shouldnt distance btw them be fixed
P is not fixed tho.
wth
It can move along the rod.
🗿
OOH
I GET IT
my dumbass thought pin is fixed
Lmao, I thought too until I saw the solution.
They prolly should have said sleeve tbh.
ye
pin made my brain think fixed
@Percy u can close now , and @Percy @SirLancelotDuLac thx to u both
+solved @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@714440046429601792> (714440046429601792)
Time
<t:1745334383:R>
Solved by
<@1075951732460376214> (1075951732460376214)