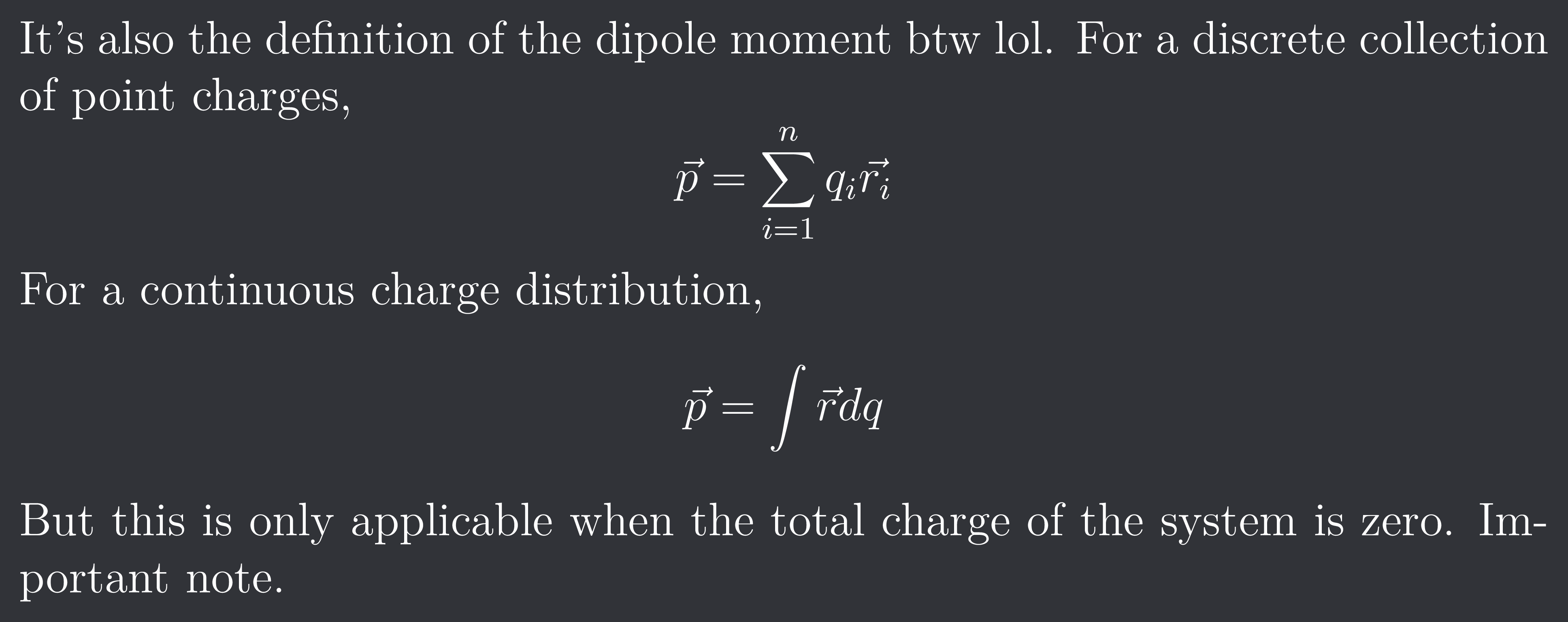Electric dipole
how do we solve the ques which have the dipole distributed in an eqilateral triangle like the ques that go electric charge q,q 2q are placed on vertices of equilateral triangle calculate effective dipole moment
18 Replies
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.You mean q,q, -2q?
q q -2q hoga
and its simple.
just make two dipoles of moment p where p = q.d
then take resultant
ig 60° pe aaenge
yep
can u tell with an exmple?
Split the -2q into -q and -q, make 2 dipoles (with -q and q as each) and add vectorally.
Or you can do the vector sum of
$$\vec{p} = q{1}\vec{r{1}}+q{2}\vec{r{2}}+q{3}\vec{r{3}}$$
Opt
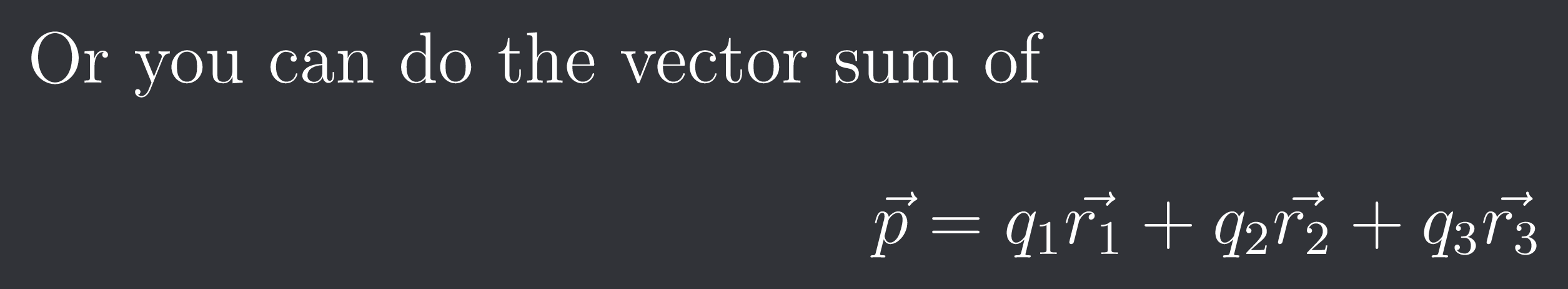
Same result
Yo how is the alignment in this latex set :thinker:
Its bigtext so supposed to be centre align
But uhhh
It looks to be right aligned
Ah I see. Because of the 2 "$"s?
Yup
Got it. Thanks.
ok this seems easier thnks
+solved @Opt @Dexter @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@888280831863451688> (888280831863451688)
Time
<t:1745224630:R>
Solved by
<@763645886500175892> (763645886500175892), <@1095655769376034818> (1095655769376034818), <@1075951732460376214> (1075951732460376214)
It's also the definition of the dipole moment btw lol. For a discrete collection of point charges,
$$\vec{p} = \sum{i=1}^{n}q{i}\vec{r_{i}}$$
For a continuous charge distribution,
$$\vec{p} = \int\vec{r}dq$$
But this is only applicable when the total charge of the system is zero. Important note.