electro
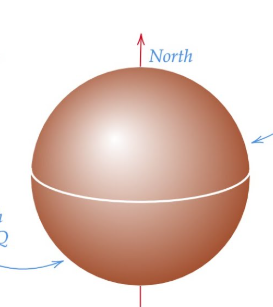
force between two hemispheres (part of a phere) with different surface charge densities
39 Replies
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.its like this but the upper has sigma1 and lower has sigma 2
This is similar to the derivation for excess pressure iirc
Oh it's different densities
yeah
pls dont use scaling
Scaling?
uh leave it for now
@Opt i hab a approach but its math is weird
consider a small area dS on hemisphere 1
now consider another small area dS on hemisphere 2 diametrically opposite
dF = $C\sigma_1 dS \sigma_2 dS$
Aetherfly
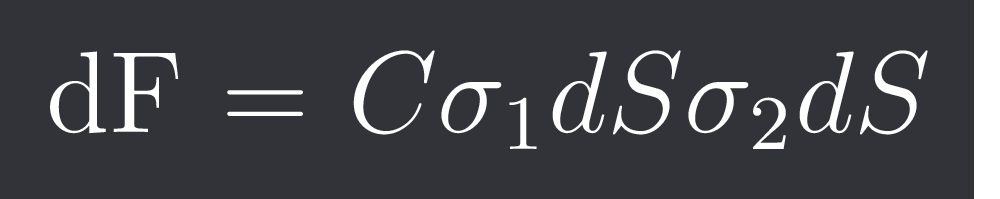
Well, it's not just diametrically opposite components that contribute to the force
Ok, random idea but, take a duplicate copy of this sphere and rotate it 180°, then superimpose with the original. The force on each hemisphere will be double the original, but the charge density will be uniform.
Ok, I tried something else and got $\frac{\pi R^{2}\sigma{1}\sigma{2}}{\varepsilon_{0}}$ as an answer. That's probably wrong though.
Opt
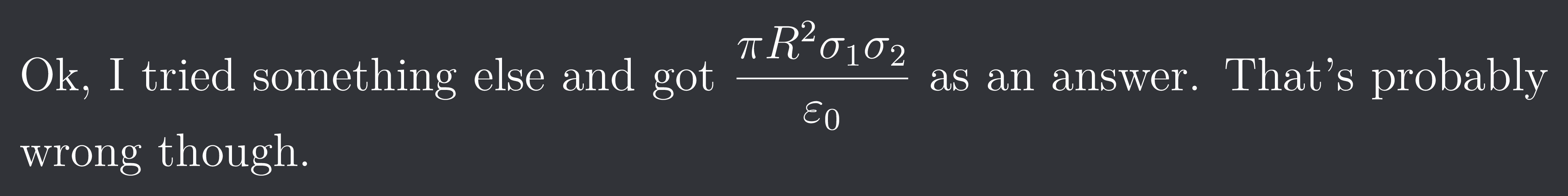
i think there is a 2 in denominator
in the ans
Is it right other than that?
ok yeah its 2
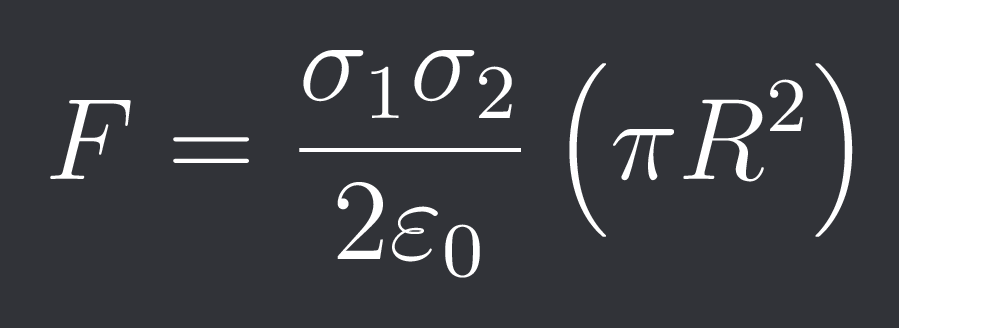
i found an approach but I think its kind of wrong
What I did was find the so called 'centre of charge'
Then force between points
centre of charge hmm
Centre of charge as in
$$\vec{r}_{C.o.C} = \frac{\int \vec{r}dq}{\int{dq}}$$
Opt
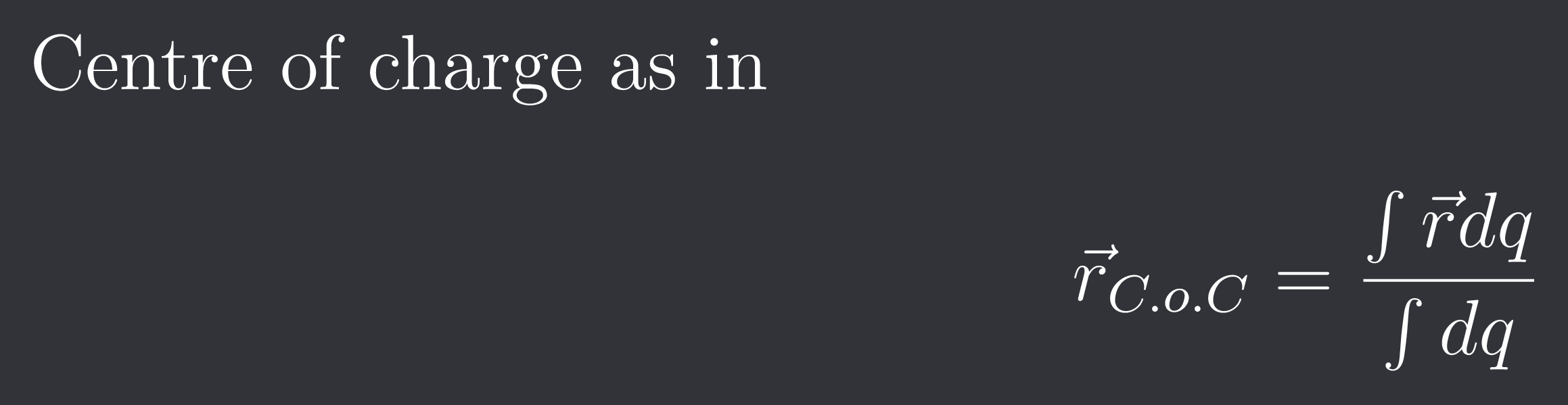
but centre of charge shouldnt work with $\frac{1}{r^2}$ field
Aetherfly

inverse square fields don't support centre of charge i suppose
Gravity is an inverse square field though?
but that doesnt support centre of mass
Oh yeah
Nvm
you cant find the force between two extended bodies using cente of mass
Yup, I got it
ok
@Opt
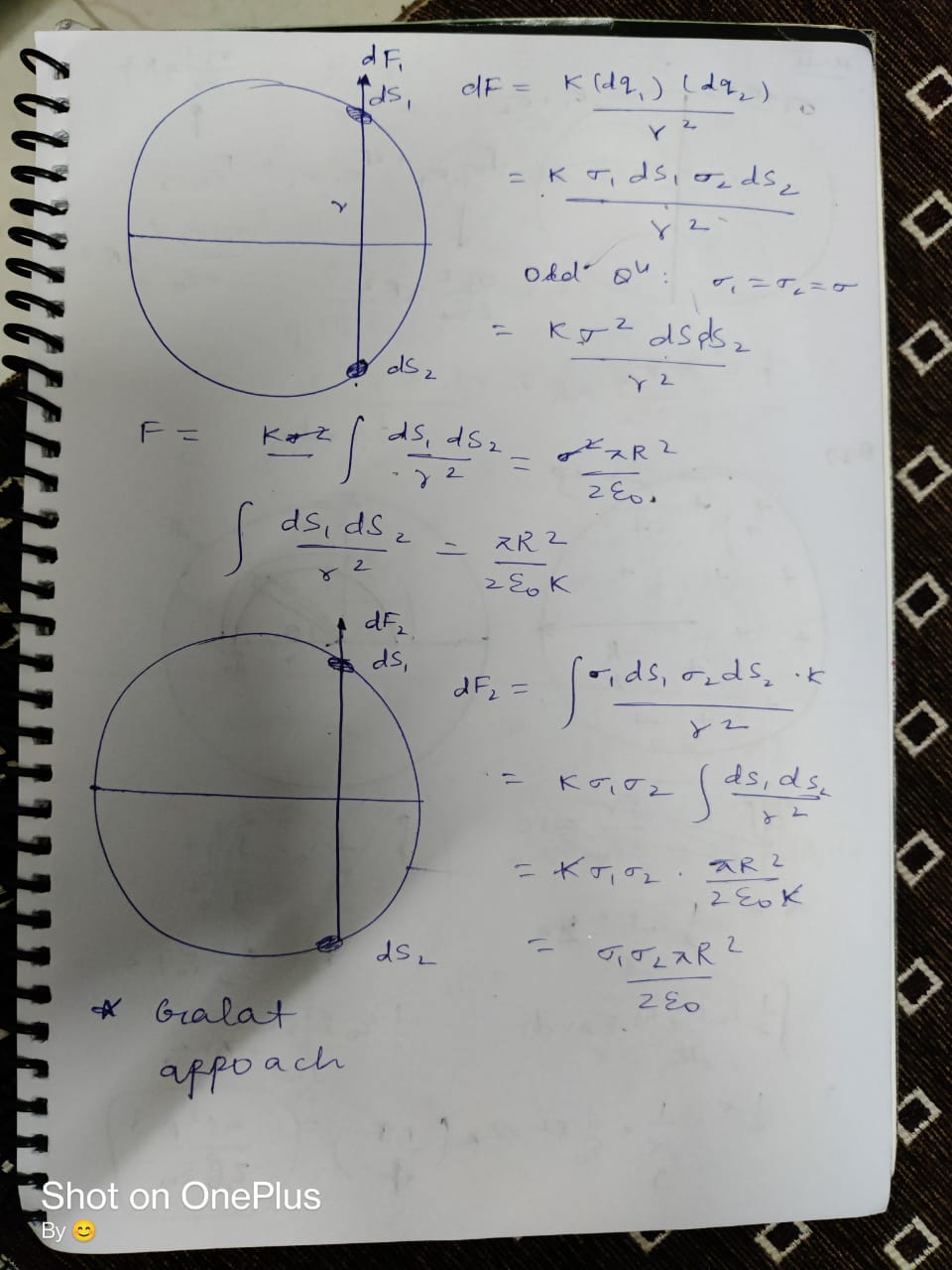
this is what i tried
ignore the bottom lef
Okay, sort of lazy but: let sigma 1=sigma 2, then electrostatic pressure*area and replacing sigma^2 with sigma1.sigma2 would give the answer.
y replace by sigma1 sigma2
scaling principle?
Yeah.
yup that works
theres another method for the qn
put a sigma2 ontop of sigma1 and a sigma1 ontop of sigma2
so its a sphere with net sigma1 + sigma2
now due to this sphere its going to be (s1 + s2)^2/2e
where s is sigma
this can be individually written
like F(s1)(s2) + F(s1)(s1) + F(s2)(s1) + F(s2)(s2)
and F(s1)(s1) and F(s2)(s2) is known
and F(s1)(s2) = F(s2)(s1)
shall I send a written soln?
No, I got it.
amazing
so whats wrong with my method is vectors
im not considering the other patch areas along with patch area 2 which would be applying forces on the patch area 1
still im getting the correct ans due to scaling principle
is that ryt?
OH WAIT
the integral of dS1 x dS2 is actually a vector integral itself
it consideres all possible areas on both the hemispheres
all possible combinations would be included in the double integral
so the former part is wrong but the latter is correct somehow
What's this scaling principle? :aah:
Here I am integrating rings and vectors and crap
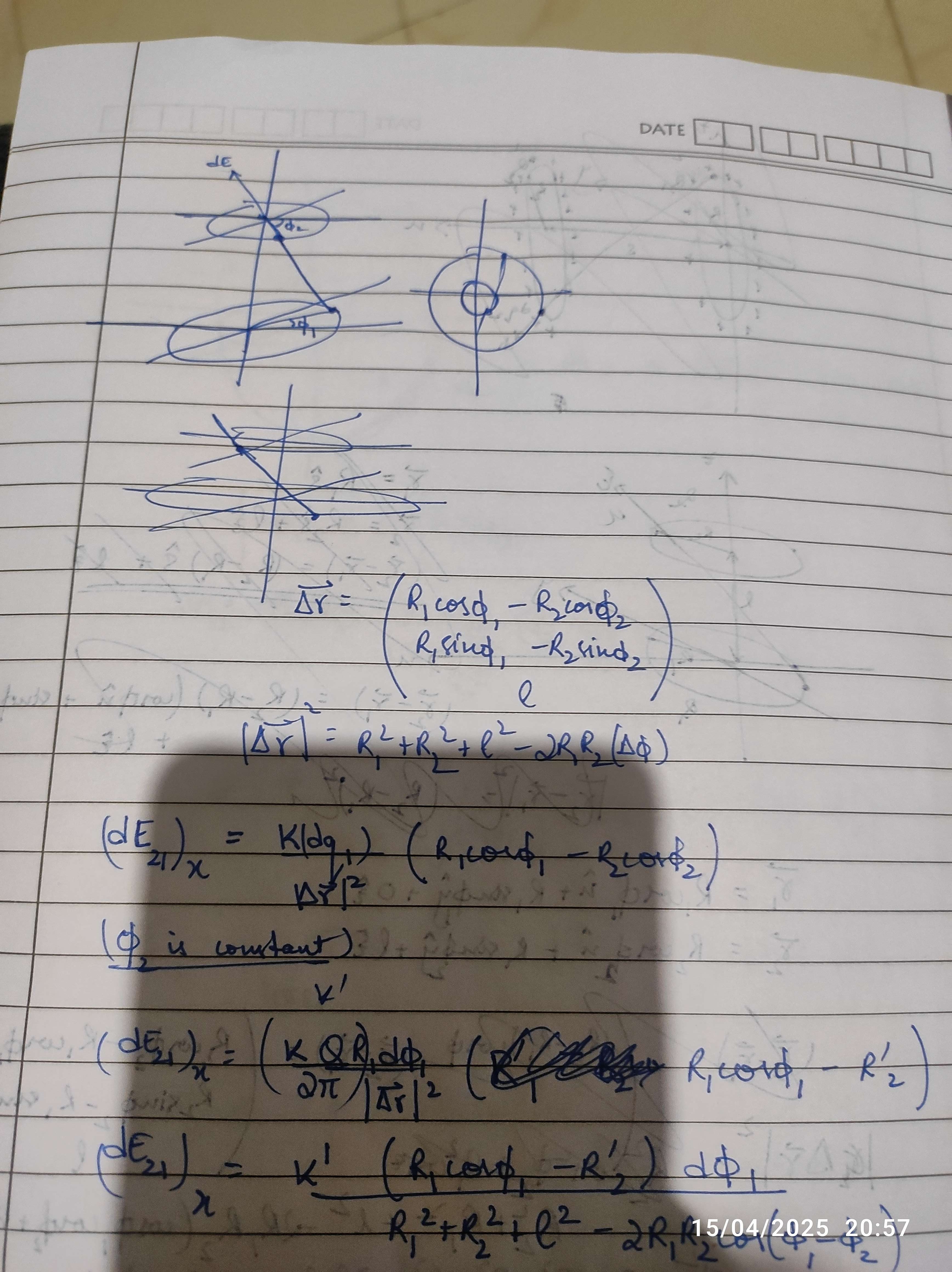
uh
so we can observe that force is proportional to product of charges
so f is proportional to (s1)(s2)
now just take ratios
wha
ok lets leave this for now