gauss law
a hollow insulating sphere contains a point charge +q are its centre, find force between them
61 Replies
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Is the insulating sphere charged as well?
yes +Q
There's no force either way I'm pretty sure
yeah sorry for being dumb but what mistake am i doing here
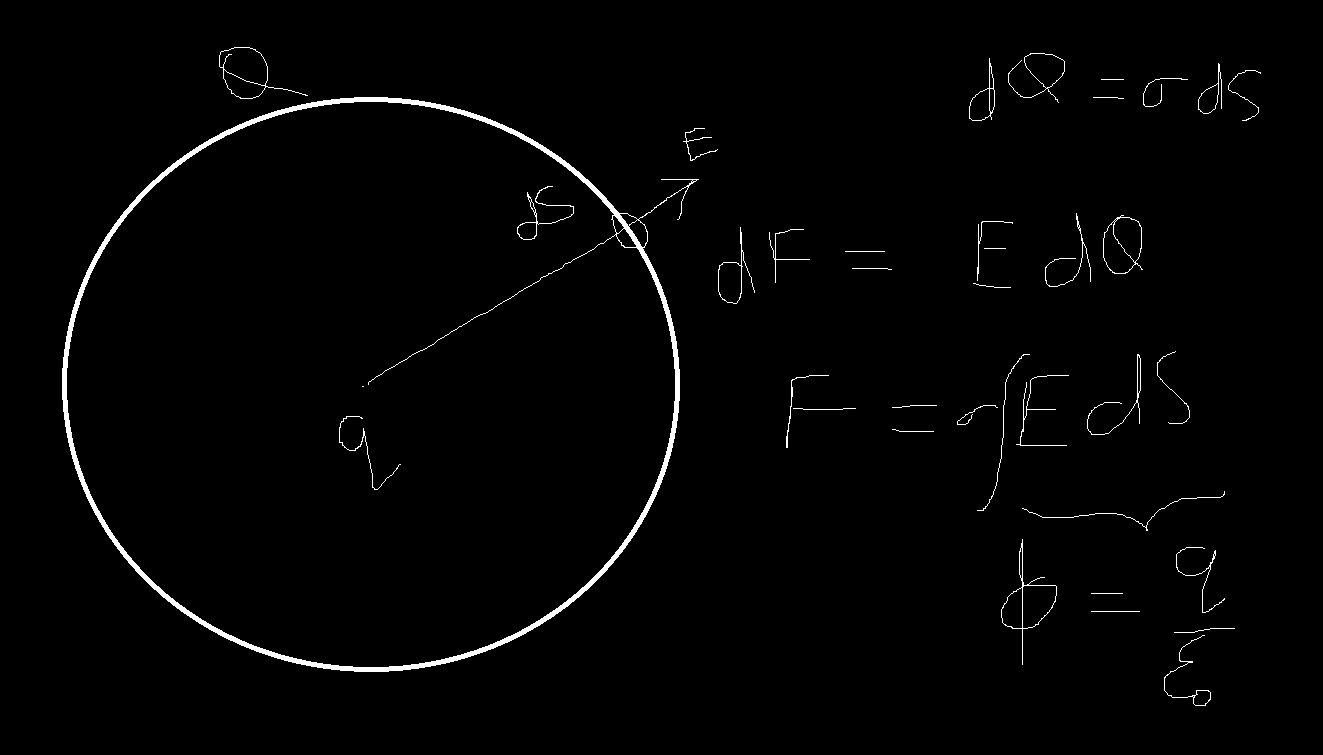
Force on point charge is zero, and by Newton's third law, force on spherical shell should also be zero
exactly
The integral thing mein you are treating a vector as a scalar.
Ah, but the thing is, ʃE dS is not flux
Flux is ʃE•dS
it should be EdS cos theta but theta = 0
E.dS doesn't add up, rather adds vectorally cancelling out.
Just the integral is zero since corresponding opposite field vectors cancel out
but E dot dS is always positive
for any dS
Yes. Here you're not doing the dot product
but uh E dS costheta = E dot dS right??
i mightve confused this with the plate qn
have you done the square plate qn?
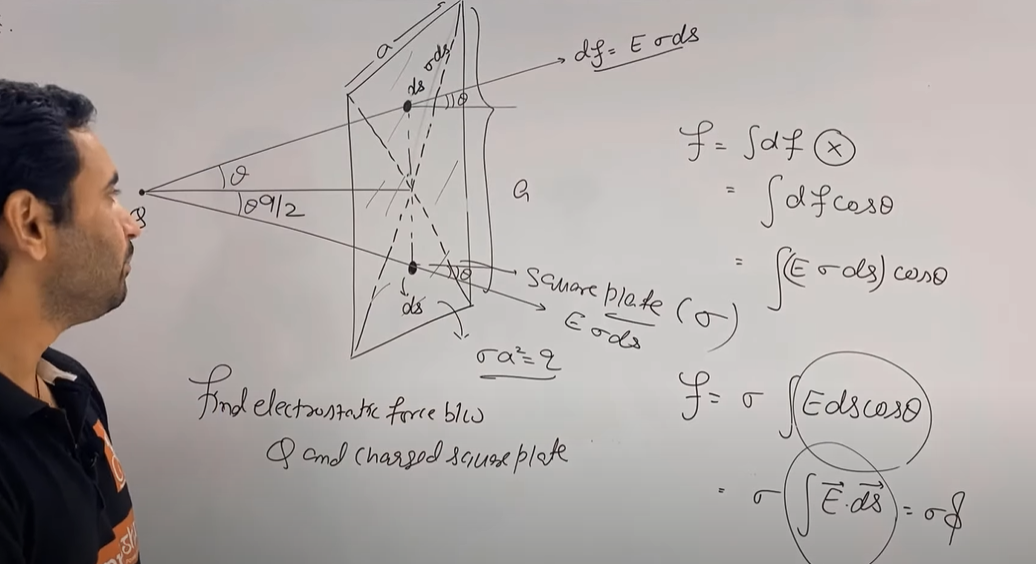
There's no cosθ here though
like uh cos theta = 1 cuz angle b/w field and dS is 0
Also, see it this way. Are you not integrating for the force?
And force is a vector
So if your answer is a scalar....
Surely there's some mistake right?
yes
And that mistake is that here you're integrating Edq correct?
Bold is vector
And dq = σdS
So that's a scalar
oh yeah
So your integral is ʃEσdS ?
The only vector in your integral is E, and that cancels out because each field line has one in the opposite direction
yup
how r we doing this
by the same logic E is the only vector here
Ok, but there you don't have fields that cancel out.
And for that question too, try doing the Newton's third law method.
but we're still writing EdScostheta = phi
Ok, so there's an abuse of notation going on there. Let me type in LaTex for you to understand better
It is correct up till
$\vec{dF} = \vec{E}\sigma dScos\theta$ and
$\vec{F} = \int\vec{E}\sigma dScos\theta$
However, converting that into flux neglects one point. It should be written as
$\vec{F} = \sigma\left(\int\vec{E}\cdot\vec{dS} \right)\hat{E}$
Where $\hat{E}$ is the unit vector in the direction of the field.
@Aetherfly
Opt

wyh is the E(cap) outside the integral
Because it's a unit vector, and the integral part is just the magnitude
oh nvm force is a vecotr
It could be inside too, but that's confusing
So while it's correct by numbers, it's missing a key component which is the vector part
hmm and the E cap is zero in our qn
but not in the square plate qn
Bingo
You're correct
No, you were right before.
The sum of all E is going to be zero
net E(cap) is zer
Yeah
thanks a lot man nahi toh I was going to spam this trick on every damn electrostatics qn lmao
Yeah, dimensional analysis is good and all but vectors are important too
ok can i use the "trick" in this qn
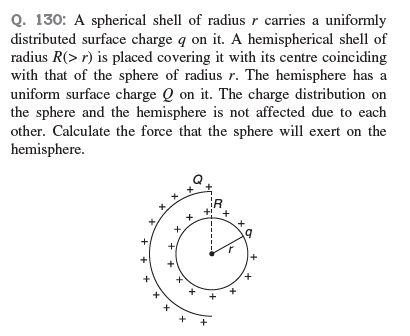
@Opt
rhe sphere can be thought of as a point charge at the centr
Yeah, you can do the flux thing here I'm pretty sure.
But Gauss' Law won't work
yeah but the flux is just q/2e right?
e is epsilo
Yeah. I suppose.
so $dF = \sigma dS E$
Aetherfly
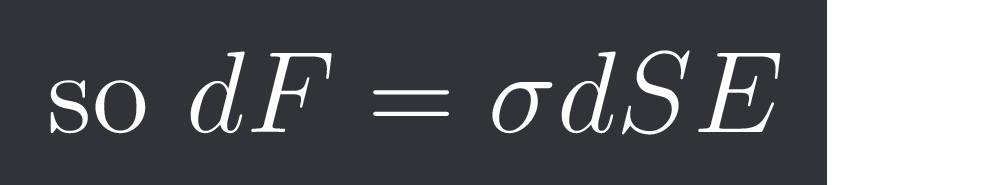
Yes, but with vector symbols on F and E
mb
$F = \frac{Q}{2 \pi R^2} \frac{q}{2\epsilon}$
Aetherfly
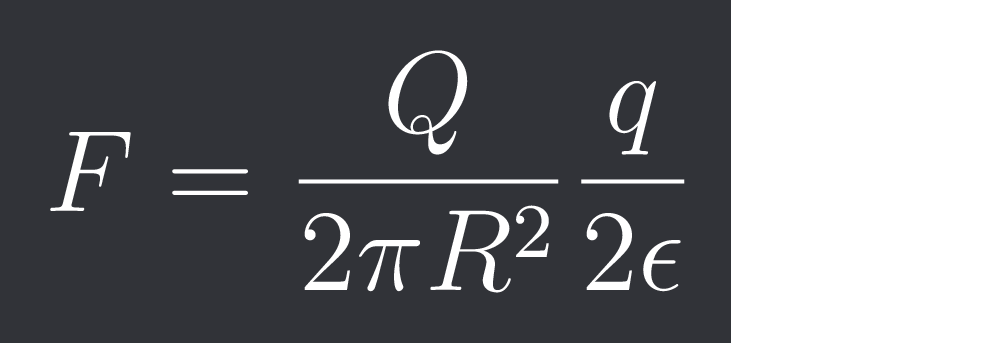
this should be corrdt
but the book says its
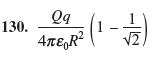
Then you're better off doing it the normal way
Tricks are only useful when they're applicable everywhere.
isnt their method incorrect?

true but they're using the formula wrongly ig
cuz the field due ti a hemispehre are the centre is sigma/4e
Their method is legitimate I'm pretty sure. But I'm not sure if you can approximate the sphere with a point when you're calculating the force on the sphere.
...you remember that?
uh yeah
the R in their method should be r
in the 1st eqn
Oh yeah
Just integrate it right and check i suppose
ok thanks

+solved @Opt
Post locked and archived successfully!
Archived by
<@831415988636614696> (831415988636614696)
Time
<t:1744548679:R>
Solved by
<@763645886500175892> (763645886500175892)