25 Replies
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.understood the solution to this point

my main doubt is why have we taken r and R as integral limits

Gimme a moment.
I'm about to get home
aight take your time
Well, I could explain it without writing it down if you want
The field stuff is honestly unnecessary
Unless field was specifically asked
What you can do is, for every position r, we can divide the ball into the charge enclosed within the sphere of radius r, as well as the charge enclosed within the region from r to R, right?
Then, we can calculate the electrostatic potential due to each of those parts.
The potential due to the inner charge is just going to be that amount of charge times 1/4πε times the distance from the origin, which is just r.
ok
ohhhh
yes
The potential due to the outer charge is going to be integrated, taking spherical shell elements.
The potential due to each shell is going to be the charge on the shell, times the constant 1/4πε times the radius of the shell, not the distance from the origin.
So, for that, we integrate from our chosen r to the maximum R, since we are considering charges outside our radius r.
I see
I have no clue why they chose to use Gauss' Law for such a simple distribution.
thanks a lot for the simple explanation
yeah they tend to overcomplicate stuff a lot
Do you want me to send the solution too?
that would be great
thanks again

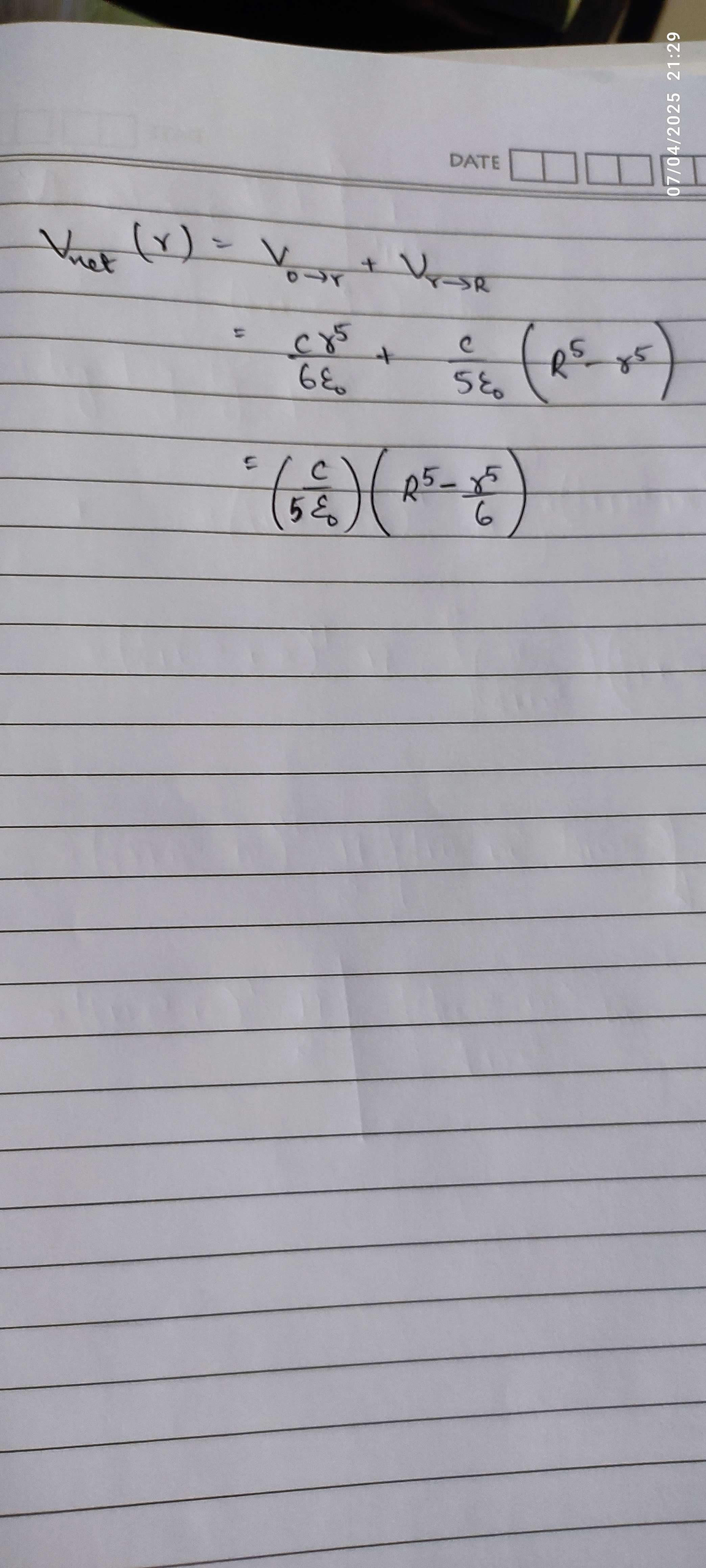
@nimblehammer 🍋 got it?
If you didn't understand something, do ask
hey so for Vr->R, you used dq/r' whereas for V0->r, you used dq/r. May i know the reason?
Ok, so, for the charge inside, you can assume each charge to be a point charge placed at the origin, and calculate potential as you would do for that.
(The proof of this can be done by Gauss' Law if you haven't learnt it yet)
But, for the outer charge, we have to use the fact that the potential anywhere inside a charged spherical shell is the same as the potential on its surface, which is Kq/(radius of shell)
ahh i see
thanks a lot mate
Got it?
If you're not sure, you can always ask one more time.
The proof for the potential inside a shell is sort of trivial
We know by Gauss' Law that the field inside is identically zero which means that the potential has to be constant. (Derivative of constant is zero)
So we consider the potential at centre, and it has to be the same everywhere else inside the shell as well.
AHH I SEE
thanks a lot g i have always faced problems when solving questions regarding spherical shell
Dw it's gonna pass with some practice
yeah i am lacking in that so trying to make up for it
+solved @Opt
Post locked and archived successfully!
Archived by
<@764395159458021387> (764395159458021387)
Time
<t:1744053953:R>
Solved by
<@763645886500175892> (763645886500175892)
