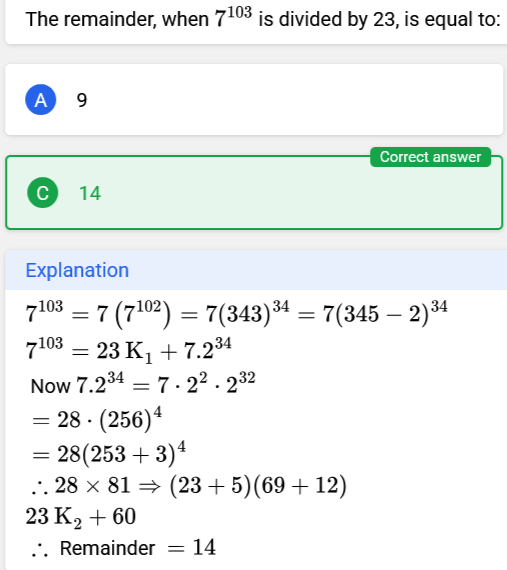
Remainder problem
What is going on here what are they tryna do
30 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.apparently i only know how to solve remainder problems when i can express it as
(p-1)^n345 is divisible by 23
So 343 = -2 (mod23)
Similarly, 256 = 3 (mod23)
There's honestly an easier way to solve this
which is?
Using Fermat's Little Theorem, a^(p-1) is congruent to 1 modp, given a and p are coprime.
So you can reduce the exponent by multiples of 22
Until you have number smaller than 22
Which in this case is 15
i dont know number theory 🤑
Then that is 343⁵ , which is (-2)⁵
Yeah, I'm no expert either
what does fermat's little theorem say
in simple words if you will
So -32 mod 23, add 46, you get 14
Answer is 14 ig
Ye
ill brb keep talking
If you have two coprime numbers a, and p, with p being prime, then a^(p-1) will leave remainder 1 when divided by p
Well, actually it's more general than that, but this statement is the most useful corollary

source?
Pathfinder
oo
how many books have u read , there is alot of stuff ic u guys talking abt which idk shit about , did u self study?
Yes for Olympiad stuff a tiny bit
wtf if this is tiny bit then wahts alot
also does this help u in jee alot or what?
Olympiad geometry
Not really
Every now and then
ic some questions only
With SnS, PnC, remainder
bascially only number thoery helps
Combinatorics too
whats that if i may ask?
PnC on steroids
ic
fancy pnc
sounds intresting i will study
@Nimboi [ping if answering] did you get this or do you want a full solution?