77 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.did it using cartesian
limits of theta should be from 0 to pi ig
From zero to what?
What's the parameter there?
x (naught)
x0
Ah
idk about r tho
what should be limits of r
0 to $\sqrt{x{0}^{2}+x{0}}$
Opt
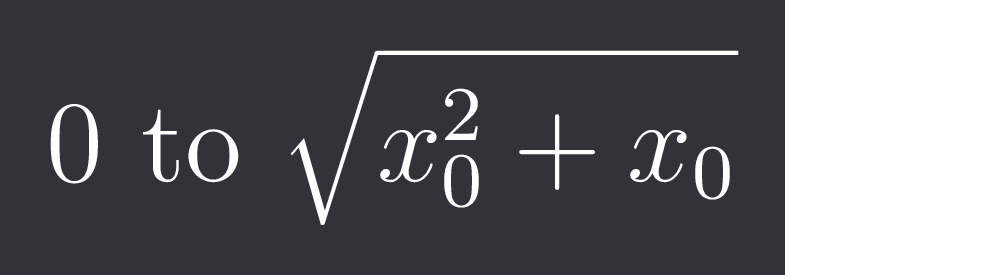
so r is independent of theta?
Gimme a moment. Why would you even want to integrate this using polar lol?
to understand better maybe
we were taught this in phy
only for 2 qns
but I believe a lot of qns can be solved related to phy easily using double integrals
(like the morning guy who tried to solve the wedge qn in g-frame)
This is unnecessarily complicated
Bud, the amount of trigo popping up is insane.
lol
like uh
the normal approach is going to a general r and general theta

and then you get a small element dr and rd
Get r in terms of theta, then integrate area element.
wow
It collapses to a single integral
r in terms of the
ehh ok but
like cant you just do it with the bounds
if you have correct bounds then the double integral is correct
I don't get you.
the area element dA = rdr d(theta)
now you just need to setup the bounds
r(min) = 0
Atp just use dA = dxdy and save yourself the trouble lol
yeah ive done it using that already
but again i wanted to know the procedure
You don't is my point.
like how did you get that
Always try to simplify it as much as possible.
r = $\frac{cos\theta}{sin^{2}\theta}$
Opt
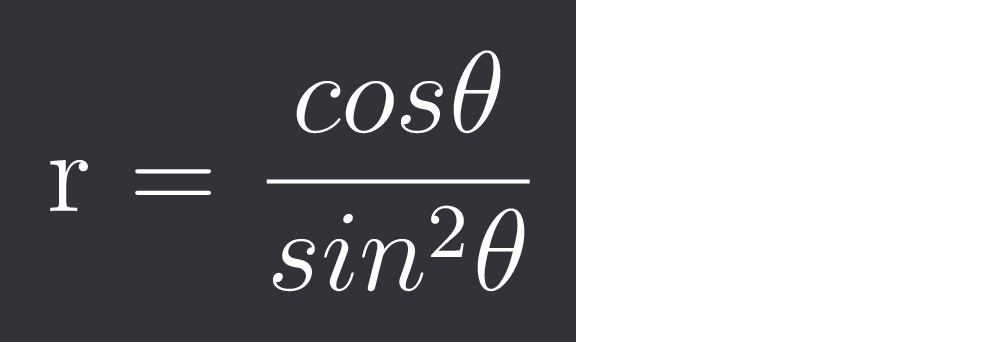
hmm
r(max)?
Take x_0 and plug in x_0 = r(theta_0)cos(theta_0)
oh
ehh maybe lets leave this one
can I ask another one here? or shld I create another thread for it?
Just ask
It's fine
ok so how do you find volume of a sphere using polar where origin is at a point on the circumderence
Are you given the parametric equations before hand or?
parametric eqn?
What is given?
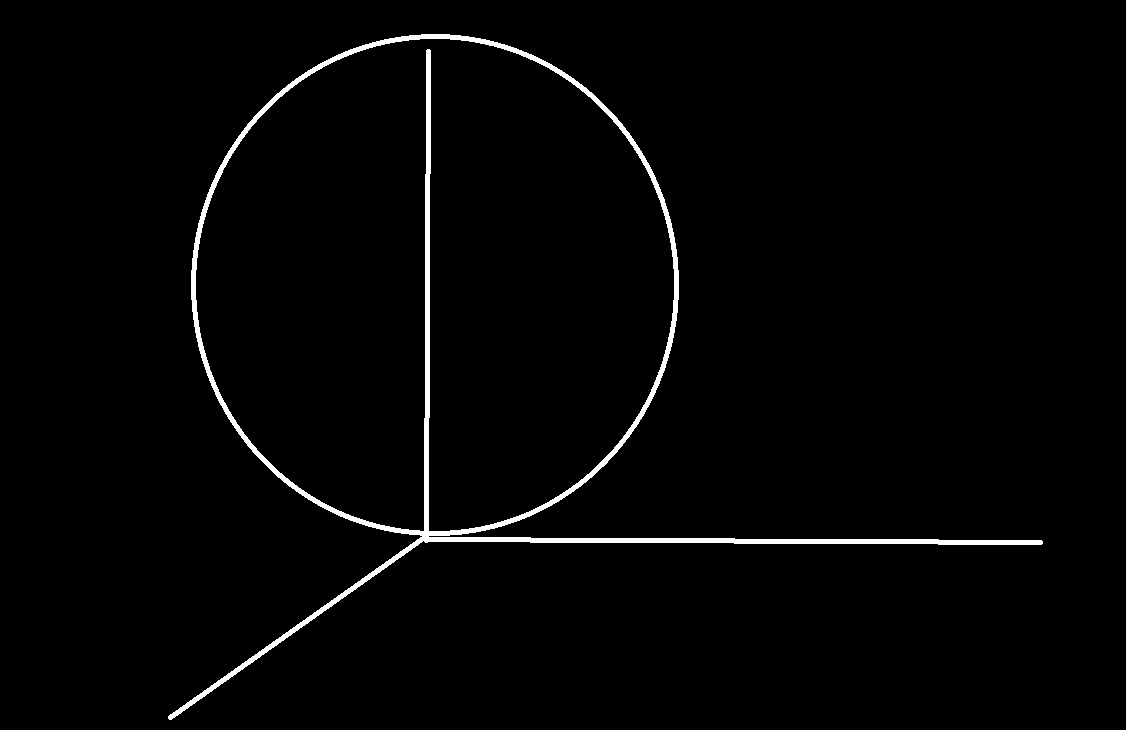
this
No, i mean, what information is given? What values?
radius is R
you need to calculate volume
using polar coordinates triple integral
Then you don't integrate......why are complicating things?
eh maybe for some electrostats
Volume is always dependent only on the characteristics of the shape itself, never its position.
yeah but potential function requires volume function
dV is always r²sinθdrdθdφ in spherical coords
Or rdrdφdz in cylindrical coords
hmm
but the bounds....
What's going to bother you more than the bounds is the element.
So what you do is shift the origin, integrate, and shift again.
Since this is a scalar integral, it's not going to change with shifting of origin
what so you can still find potential?
what if charge density is non uniform?
but the element is just the rd(theta)d(phi) thing ryt
so dQ = (rho)dV
Yeah, I'd you have ρ in terms of r,θ,Φ, it's all well and good.
Also, r²sinθdrdθdφ
why the sin theta?
oh wait theta is from z
It's dr(rdθ)(rsinθdφ)
You should try and figure out why
yeah
i frogr its from z
yeah
now just the bounds
theta from -pi/2 to pi/2
phi from 0 to 2pi
r from zero to 2Rcos(theta) ??
No, theta is always 0 to π
r from 0 to R
wait but the origin is at circcumference
of the sphere
Oh right
so r from 0 to R, theta from -pi/2 to pi/2 and phi from 0 to 2pi?
0 to π not -π/2 to π/2
You're gonna get volume of the sphere either way
sad
so the bounds are wrong
The bounds are irrelevant if you're just integrating dV
how tho
this doesn't happen in case of a circle
See the thing is, you'll never be integrating like this. It's inefficient
but there is a qn in physics for a circle
so why not for a sphere?
I don't understand your question
find the potential at the circumference of a uniformly charged sphere (using integration?)
ive done a similar qn but it was a disc instead of a sphere
Ah, so, what do you do is, integrate the potential due to each spherical shell element with the centre of the sphere at origin
Here it's spherical symmetry
ok but cant we do this using triple integral
I'm asking why you would want to do that lol
Use triple integrals when you need to
cuz ive done a similar one with a disc using double integrals
Why waste time and effort?
When there is a simpler and more elegant method?
You're basically asking why we can't knock down the door with a battering ram when you have a key
hmm
this works even for weird densities ryt
Yup, as long as it's spherically symmetric
hmm what if its not
Gimme an example
i need to find one which is integrale
hmm
ok what if you already have origin at the circumference
rho = Kr^2
thats symmetric too
ok what if you need to find potential inside a hemispherical shell at distange r along its axis
ive seen a qn like this
ill think about this
Use cylindrical coords. You have symmetry about z axis.
o yea can be done using single integrals
Yup