electrostatics
A square of side b centred at the origin with sides parallel to axes x and y has surface charge density σ(x,y) =kxy (where k is a constant ) within its boundaries. Total charge on the square is?
The ans is 0 since positive and negative charrge desnities cancel out...but how do i do it with integration?
28 Replies
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.wow
Q = $\iint_{\lvert x\rvert,\lvert y\rvert\leq\frac{b}{2}} \sigma(x,y)dxdy$
Since $\sigma(x,y)$=kxy is odd about X axis, and odd about y axis, the integral from $\frac{-b}{2}$ to $\frac{+b}{2}$ of it is zero in both cases. Hence, total charge is zero.
Opt
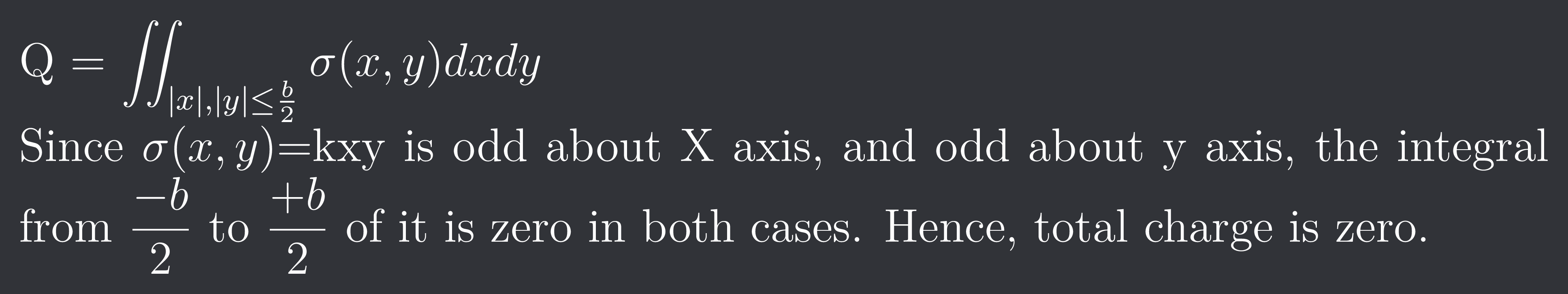
hmm but douvble integrals are not in jee
Here they commute so order is interchangeable, and they're separable.
So it simplifies to two single integrals
yeah
Both of which are zero
still they don't usually teach it in normal batches
you wont get the exact idea ig
That's why it's simple to just go by the symmetry argument instead of integral
yup
But OP asked for the integral. So I gave integral 🤷♂️
hmm I wonder if there is some way to do it using single var
calc
No,I don't think so since there's no radial or azimuthal symmetry.
There's two axes of anti-symmetry rather
wait there is a fn of square ryt?
or no?
nvm how can a square be a fn
hm i didnt understand..what does odd about an axis mean 💀
σ(-x,y) = -σ(x,y)
And
σ(x,-y) = -σ(x,y)
ahh
So, you end up getting negative charges in second and fourth quadrants, and positive in first and third.
If k is positive
And reverse if k is negative
Yeah, symmetry argument simplifies it. Integration says the same, but if the distribution is more complicated, it's gonna be a headache.
alright
eh @Opt do you know double integratn?
And triple. To some extent. I've done Calc 3 and vector calc.
Need to move on to Real Analysis
alr i have some doubts shall I create a thread?
Sure.
so if suppose centre wasnt origin, double integration would have to be used
If it wasn't origin, and the function remained the same, then yes
But in cases like these, what you can do is split the integral into the x part and y part, and multiply later
okay i guess i'll be able to do that when integration is taught in maths 😭