22 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Oh crap they're not coprime. They share 7 as a common prime factor
@SirLancelotDuLac you're the NT expert here.
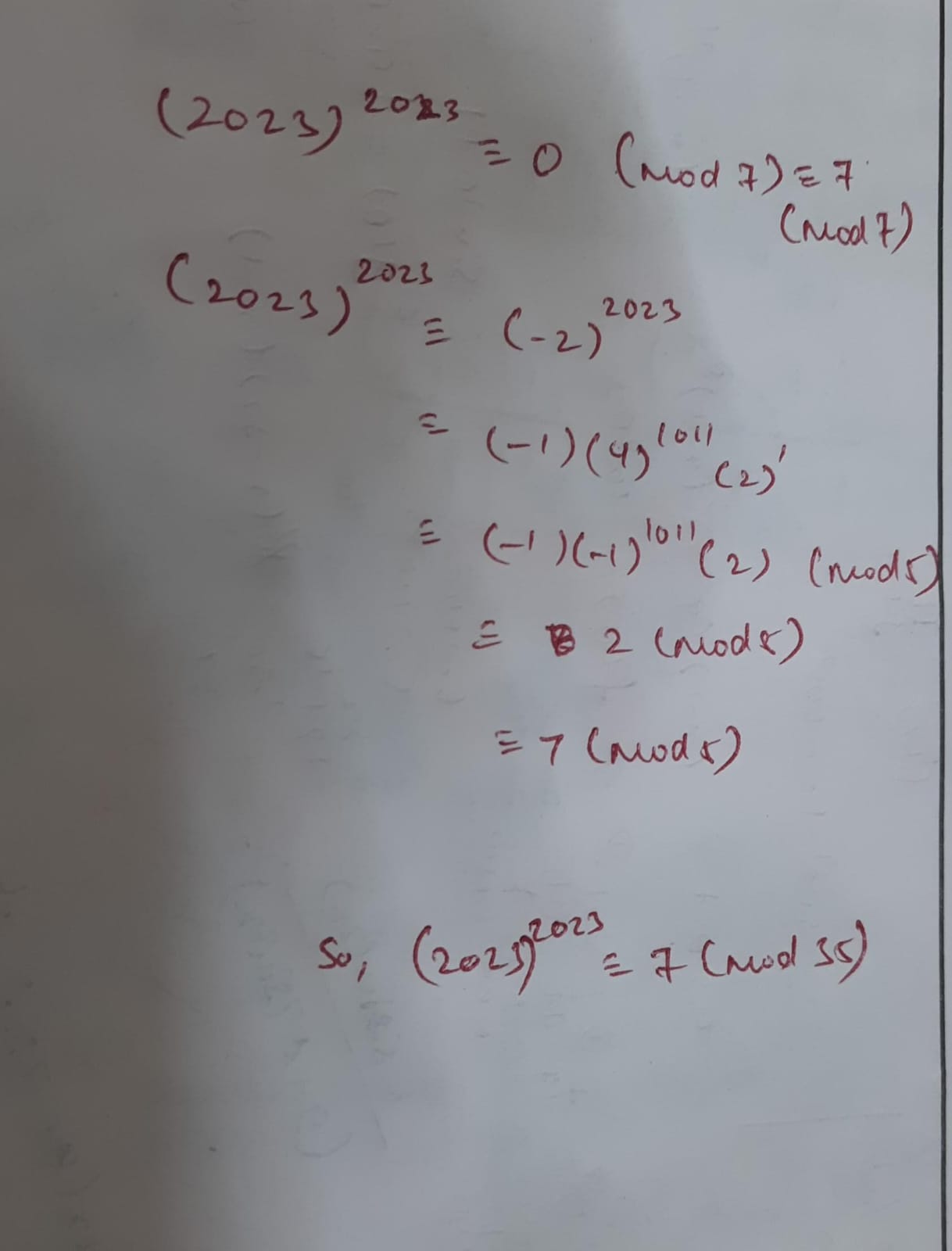
Oh, one more thing, the modulo 35 for 7, goes in cycles of 5, and 17 in cycles of 3
What's the index for your second line? Modulo what number?
mod 5
CRT keeps tripping me up.
how did mod 5 become mod 35 suddenly
all clear upto second last line
Ye sorry. we have this number congruent to 0 mod 7 which is 7 mod 7 and congruent to 2 mod 5 which is also 7 mod 5. So by CRT, the number is 7 mod(7*5) (as 7 and 5 are co-prime)
CRT referes to chineese remainder theorem?
can u state it once i am not aware of it
Yup.

What does (ni,nj)=1 mean
How to interpret it?
It means the GCD is 1. They're coprime.
Oh okay
is there some good video on this?
they only taught us the bt method
Yeah, in jee syllabus only binomial method is there. But if you are familiar with congruent arithmetic, you can look up books like pathfinder (Or some less detailed material if you want to see theory only for jee) or lectures to refer.
alright thanks
how does the imply we can just multiply mod ni and mod nj values
No, we can't multiply the values but if you can some some value a such that a1=a2=...an=k then you can say that x is congruent k modulo n1n2....
so given number when divided by 7 gives remainder 7 , when divided by 5 gives 7 , so upon division by 7*5 is must give 7 too ??
x=a (mod n1 )
x=a (mod n2)
then x=a (mod n1n2) given n1 and n2 are coprime
correct?
Yup
