Maximum Height of a Ballistic Pendulum
Consider the given ballistic pendulum. For the given setup, no torque is present on the sphere w.r.t the center of the sphere, so shouldn't the rotational component of K.E. be zero?
17 Replies
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.I'm getting $\frac{mv^{2}l^{2}}{2gI}$
Opt
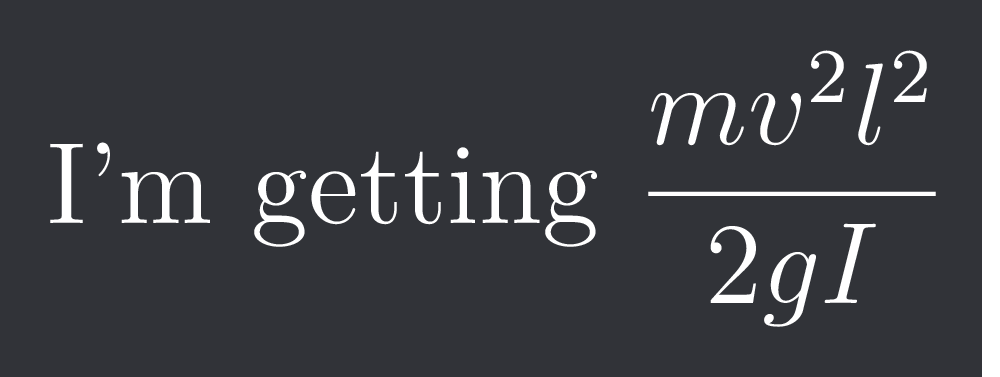
Where I is moment of inertia of the system about the point of suspension
Yep, that is correct but that would mean some rotational part of K.E. also right? Where does that come from?
It is rotating about the hinge point right?
Think of this as a pendulum with a solid rod instead of a string.
The system(sphere+block+rod) itself has a rotational KE, but the (sphere+block) doesn't. The linear KE of centre of mass of the combination of sphere and block is the same as the rotational KE of everything taken together
Doesn't it then work out something like this?
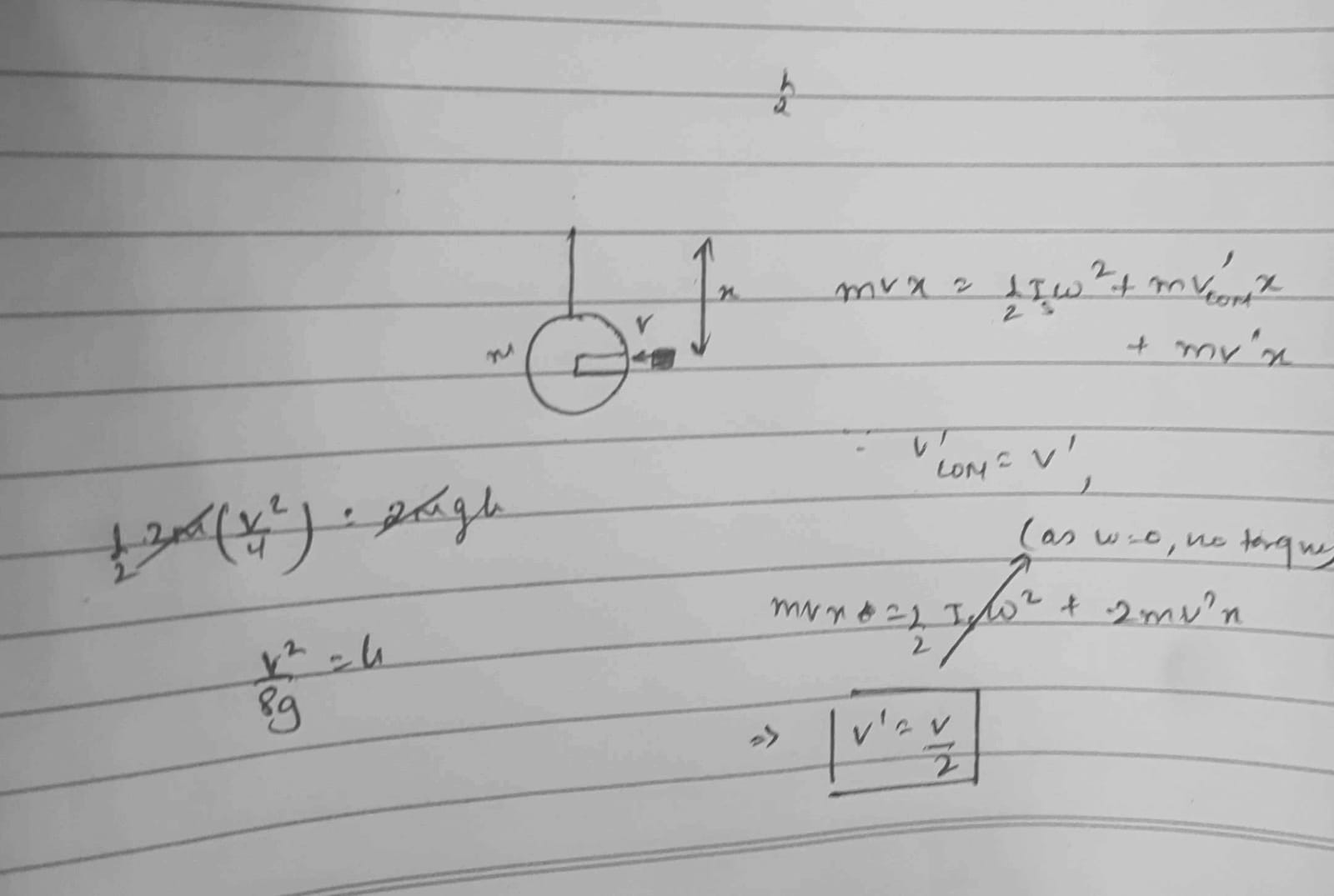
v' = v/2 is right, but as they rotate, there is torque due to gravity right?
mglsinθ begins retarding their rotation
But not w.r.t centre of mass?
Wrt to hinge
Wait, but when writing angular momenta of the system, we write L(system w.r.t c.o.m)+L(c.o.m about the chosen point) right?
Yes.
So, if there is no omega w.r.t C.o.m, doesn't it just become L(c.o.m about the chosen point), which is mvx/2?
But you can also write it as Iw
which is (I_s+mx²+mx²)w right?
By parallel axis theorem, the I of sphere about hinge is I_s + m(distance of COM from hinge)²
Ah I see.
Oh right, there would be some omega.
+solved @Opt
Post locked and archived successfully!
Archived by
<@1075951732460376214> (1075951732460376214)
Time
<t:1743301228:R>
Solved by
<@763645886500175892> (763645886500175892)