40 Replies
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.and if its non zero then how do you solve the qn?
it should be zero right no firction and the velocity is constant
yup but its not
what exactly is the external agent doing here ?
pulling spring with constant speed
and to do that its always = kx
agar lets say work ho raha hai toh WE theorem me us force ka bhi consider karna padega work
which would not give the correct ans
yep
yep
but what work did the external agent do? thats my qn
yeep
ok
ys
its true that the force has done some work
but what work is it
and why dont we add that in WE theorem
and 1/2mv^2 as well
Uh
yeah 1/2mv^2 as well
egh
but ultimately external agent
is the one which causes the spring to extend and give KE to blovck
so WD = 1/2kx^2 + 1/2mv^2
by ext agent
yes
ok
@Aetherfly It's not zero. It'll be equal to Mu^2. And you'll be able to arrive at the ans using this as well. Basically Wext = chnage in pe+ change in ke... change in ke is 1/2mu^2 and change in pe is 1/2kx^2 where x is the maxm extension. maximum extension occurs when all of the ke has been changed to pe so x= uroot(m/k). put this value of x in the wext formula to get mu^2
yes even I got this ans
but
why does this expression not come in WE theotem
work done by ALL forces = change in KE
yeah so Wext - 1/2kx^2 = 1/2mu^2 (we theorem wext + wspring= chnge in ke)
which is again the same thing
u just have to put x in terms of m and u to get to the same exp
but using that you wont get 1/2kx^2 = 1/2mv^2
you will cuz you can again find wext = mu^2... putting the same thing in that eqn u again u end up with 1/2kx^2=1/2mu^2
wait
WET says that work done by ALLLLL forces = change in KE
yeah so we include the external one and the spring force
so WD by spring + WD by external agent = change in KE of the system
yes
yeah so Wext - 1/2kx^2 = 1/2mu^2 (we theorem wext + wspring= chnge in ke)
yes
how do you have 1/2mu^2 = 1/2kx^2 then???
you'll have to substitute x
maximum extension occurs when all of the ke has been changed to pe so x= uroot(m/k). put this value of x in the wext formula to get mu^2
so you'll get wext= mu^2. if you put that in we theorem again it'll give 1/2mu^2= 1/2kx^2
how do you derive this using any of the theorems
well there's this formula that wext= chnage in ke+ chnage in pe
since here energy is not conserved we cannot say that all KE changes to PE
yes
so how this?
it's the condition for maximum extension
we're not conserving energy. we're just using the condition for maximum extension
another way to think about it is imagine you're in a ref frame that moves with u in the same direction. you'll see the spring at rest. and you'll see the block moving
y the spring at rest tho?
i saw a similar q in physics galaxy
wait a min
i'll just send the soln
they've solved it by using another ref frame
and then applying energy conservation
alright
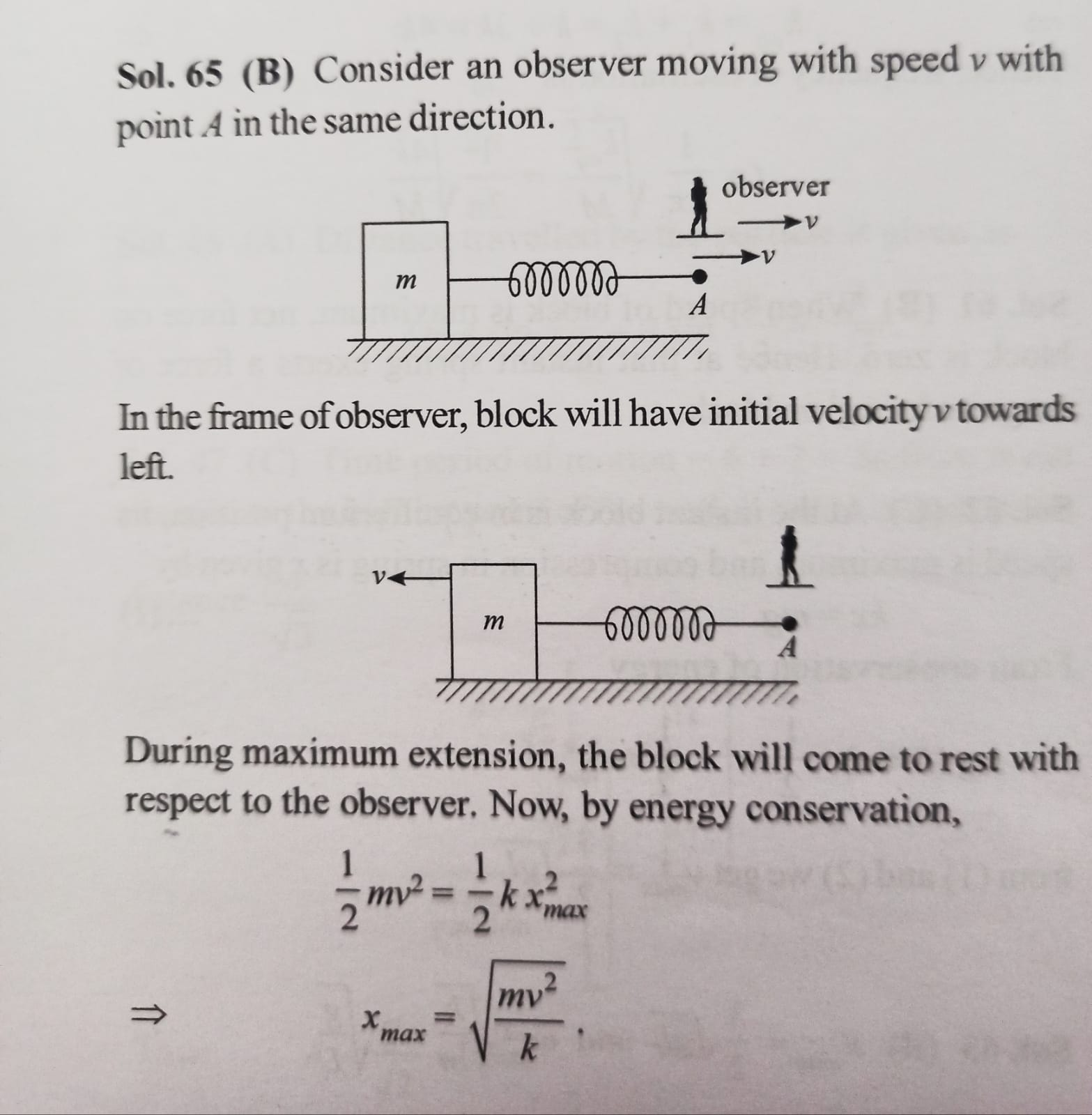
what happened to the force in this frame?
the force is still there cuz that doesnt depend upon ref frames. but we dont account for it since we see the spring at rest. the change in the ref frame has simplified the problem so using energy conservation isnt really a problem. your doubts are really good. i know this may not be a convincing explanation but yeah.
yeah quite hard for me to understand
okay maybe this will help. ext force like you pointed out earlier is kx. kx= -mudu/dx you can integrate it from 0 to x0 where x0 is the maximum extension. the limits for velcoity of the block will be from u to 0. so this gives us 1/2kx0^2= 1/2mu^2
this is in the other frame of ref
hmm the fact the the maximum extension is actually the displacement of the block is smart to use here
but difficult to see
yeah
cuz in mvdv/dx, x is displacement of block not extension
yeah but they'll be equal if we consider the frame to be moving
yeah
hmm
@ns I wonder
if there was some mass "m" which the force is pulling
WD by force + WD by spring = change in KE of the system
hm but that can be easily done in COM frame right?
yeah
