thermal conduction
how to solve this . i designed the question on my own inspired from infinite resistors ladder problems.
consider lower rods to be highly conductive . i.e zero thermal resistance
(like a wire in circuit)
34 Replies
@Dexter
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.@Moderator pls ping phy one
@Gyro Gearloose
i have solved infinite ladder with same repeating units but here the resistance is decreasing continuously by a factor of 2
we can do that
damn
no, hes a mod lol
oh lol
me fr ;-;
this is just sad
anyways i have no idea how to do this
seems very intresting tho
solution mile to ping karna please @hardcoreisdead
so here the repeating unit, instead of being R, would be R/2 right
actually wait lol
i = V/R, and R = l/KA
i.e. i proportional to K, which just keeps increasing here
i think you've made an infinite current setup
not exactly
infinite ladder ye
lowkey true 💀
no like the question you've made
you asked for net heat flow
instead of equivalent resistance right
yeah that deltaT/thermal resistance
oh im tripping wait
lemme actually use pen and paper
so in short u have to solve infinite ladder only
this isnt the same method as infinite ladder
this doesnt have a repeating unit, just a pattern
yeah it looks like infinite ladder but it isnt really
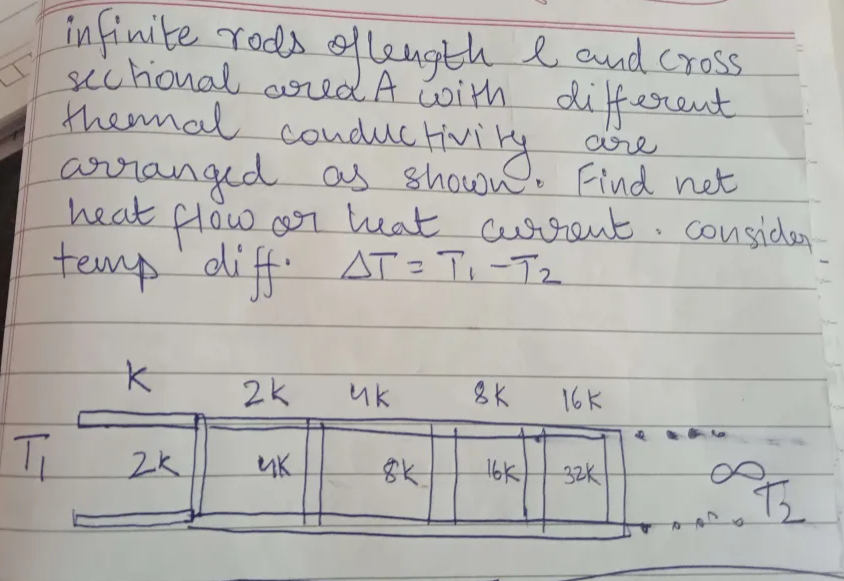
neeche waali rods bhi k 2k 4k 8k..... follow kar rahi hain kya?
forgot to mention...
consider lower rods to be highly conductive . i.e zero thermal resistance
(like a wire in circuit)
wouldn't the majority of the heat will flow through the lower rods then?
heat current should become infinite
Infinite na? Series diverges
@ᴘɪᴄᴄʜɪ | 🎧 🎶 pls? look into that error
we are getting rate limited
must be some function which sends requests every second tbh
Lower rod conductivity is k,2k,4k...?
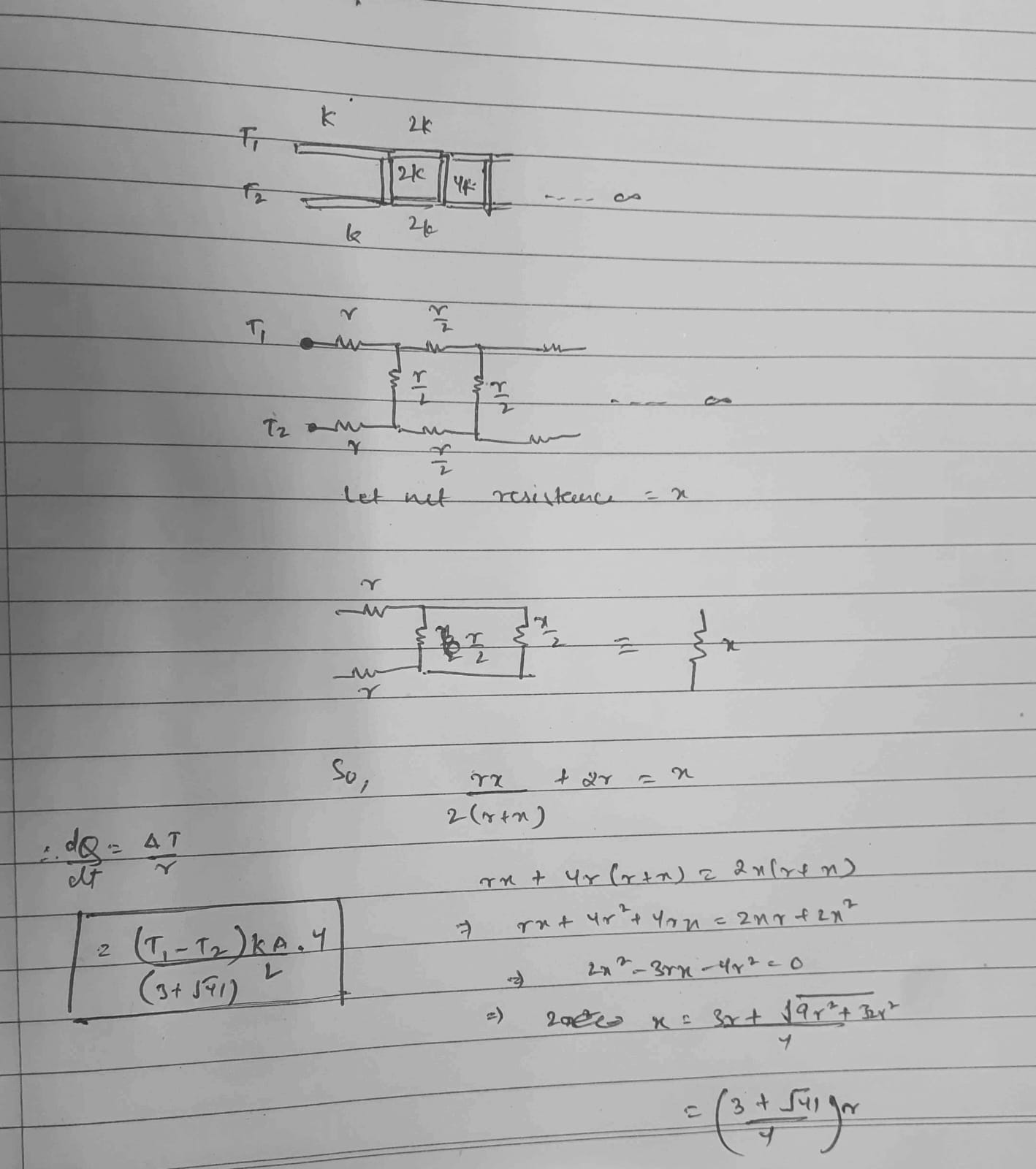
What is your basis for considering that the rest will be x/2?
We are scaling all resistances to half their value. Also, I considered T1 and T2 at upper and lower rod otherwise the result diverges.
If purely conducting rods are used, same approach to find the value ig.
they have high conductivity so zero thermal resistance
this tho. pls clarify this
If you consider the point at T2 to be at infinity, converting to the electrical analogy, you can see the points are short circuited due to them being connected by conducting wires, hence effective current tends to infinity.
Ah, then same proceedure, just the lower portion as conducting wires.
i was inspired from this problem
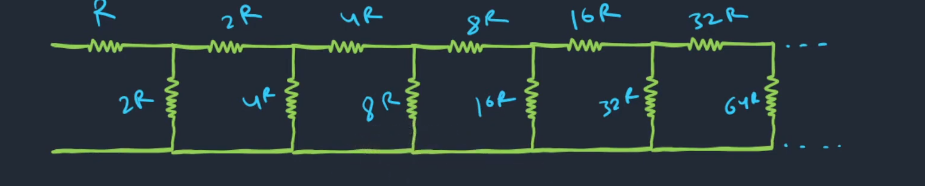
problem is in my question the resistance is getting halved . so idk the answer...
Isme starting ke dono ends different potential pe honge
Na
This is what is done here. (Approach for both will be the same)
i dont understand r/2 wala thing here
r is net resistance or resistance of that resistor
Let the net resistance of the entiire thing be x. Now you are scaling down each resistor by a factor by 2. So the effective resistance of the entire portion after the verticle r/2 resistance is x, but scaled down by 2. (r=L/k.A)
Then you get the above setup hence answer.