41 Replies
Substitute x²=t and do partial fraction stuff.
oh shi u right
$\frac{dx}{x^{3}(x^{2}+2)^{2}}$=$\frac{dt}{2t^{2}(t+2)^{2}}$
SirLancelotDuLac
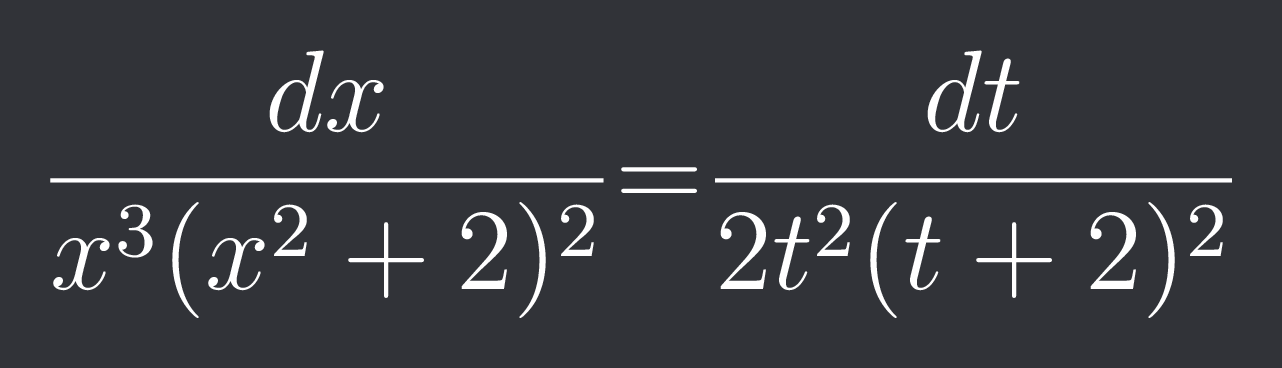
yeah that works out really nicely
the solution did this
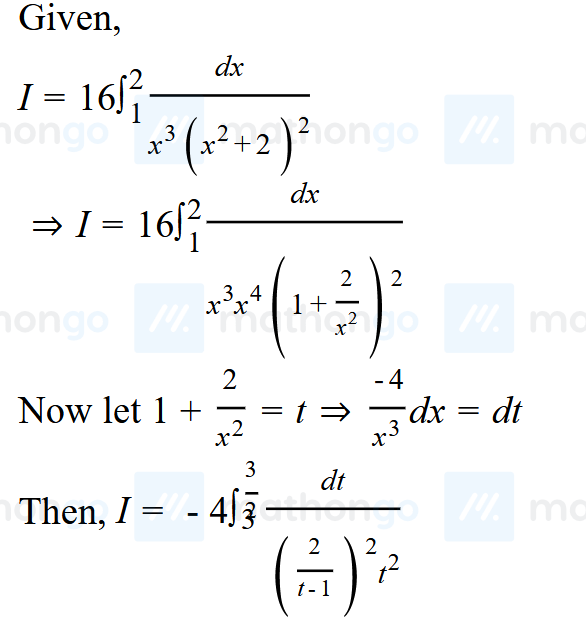
which is uh
🤷 idk how i'd think of that
partial fraction method makes total sense tho
Man, this seems lengthy tho...
partial fraction is always lengthy
what is going on here
why this
i personally would've seen the x^7 term and just dipped the other way
Idk that seems non-intuitive af. (The solution)
It works out this way by substituting x^2

so would you split fractions as $\frac{A}{t^2} + \frac{B}{t+2} + \frac{C}{(t+2)^2}$?
Nimboi

Rather than using the A/() thing, ig it would be better to do it this way...
what exactly did u do
But hypothetically if we were to do that, then that would have been length and we would've needed e/t,d/t^2,c/t+2,at+b/(t+2)^2.
oh 💀
Write 4=(t+2)^2-t^2-4t
Then simplify so you get that.
Which are all in "standard form".
(The last one is 1/x(x^n+1) form where you take x^n common from the brackets.)
ohhh
is this similar to what we do in telescoping sums
ah yes its that
Oh no wait its not that...
yeh no power term on the bracket
but this trick was very kool
Ye but it is easier to partial fraction that ig.
A/x + B/(1+x^n) directly?
oh right this is useless
Sure, $\frac{a}{x}+\frac{b}{(x+2)}+\frac{cx+d}{(x+2)^{2}}}$ here.
SirLancelotDuLac
Compile Error! Click the :errors: reaction for more information.
(You may edit your message to recompile.)
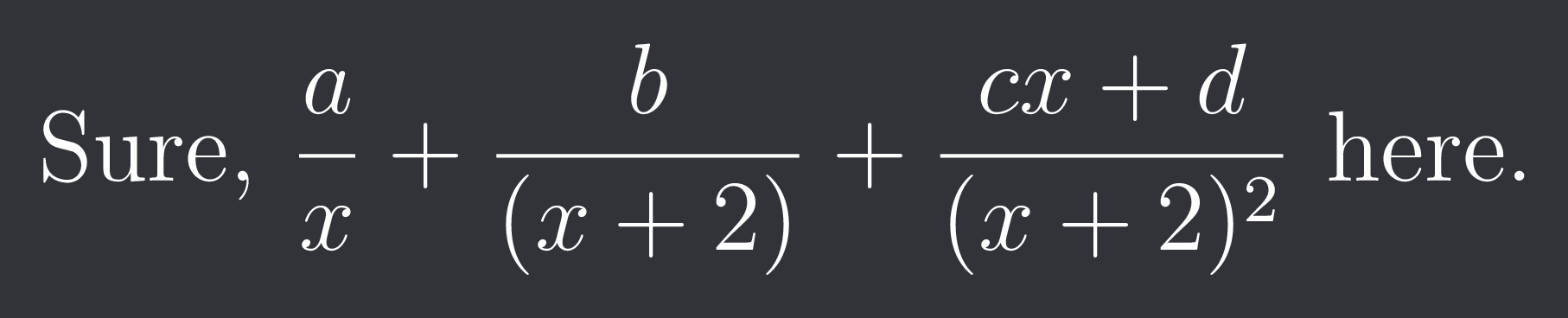
goddamn what a question
lengthy tho
thanks dude
i wonder if the bot's back
+solved SirLancelotDuLac
Can you keep this thread open for some time please?
Idk the solution we have at hand didn't seem much satisfactory for some reason...
yeah sure lol feel itna nhi aaya
it might boil down to just making this somehow intuitive
Yeah, I do see how that solution works but is not very intuitive for some reason.
the x^3 gets cancelled by 1+2/x^2, that's a fair line of thought
as for the x^4
Replacing it by the substitution they made.
i mean yeah it makes total sense lol but i wouldn't have thought of taking x^4 outside
well, maybe
Yeah. Partial fraction easily does this but its gonna be calculative ig.
i guess the thought that goes through ones mind is
"x^2 doesnt cancel x^3 but 1/x^2 sure does"
and then you just roll with that
though you dont think of x^3 as the problematic term initially, so you dont particularly try to eliminate it
True.
call @Satya S sir edkhiye ye ganda integral solve karra
correct ✅
Video idea mil gaya lol
Tum logon ke solutions copy kar lunga evil laugh
W
