Integration and limits
My approach was writing it as $\frac{\int_{x}^{2x}{\frac{sin^{m}(x)}{x^{n}}}}{x} \cdot x$ and then approximating the fraction thing to derivative of integral of $\frac{sin^{m}(x)}{x^{n}}$ which is that function itself, but unable to go on from there.
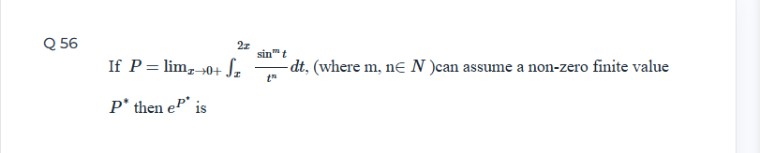
6 Replies
SirLancelotDuLac
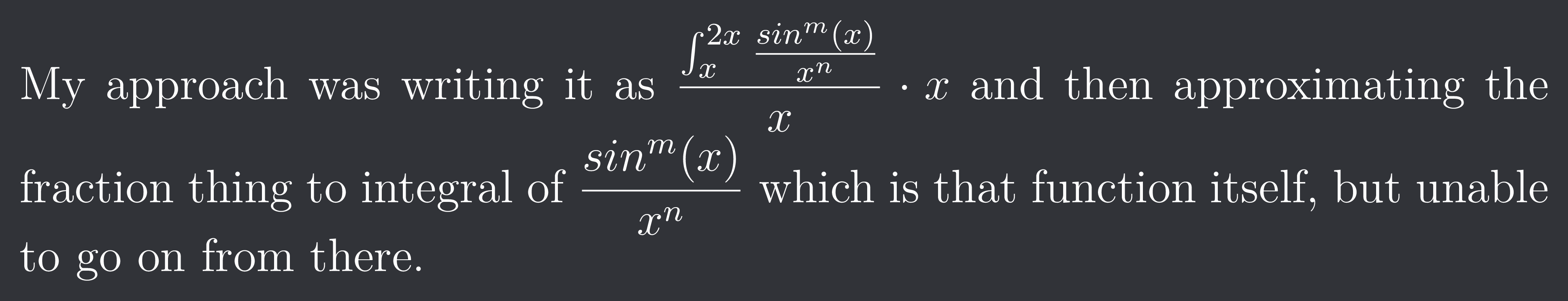
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.i dont see a method to do this properly.All i can think of is sint ~ t when t appraches 0 after doing that also you would have to take cases m-n>1 m-n<1 and a case where m-n=-1 when m-n=-1 you get ans as 2 other 2 cases you get 0 or infinity
Oh right. That works.
+solved @hithav
Post locked and archived successfully!
Archived by
<@1075951732460376214> (1075951732460376214)
Time
<t:1742818362:R>
Solved by
<@726641475080683522> (726641475080683522)