15 Replies
multicorrect ☝️
a and c?
if u think about it, a rectangle can be made
the 4 points all equidistant from origin and sum of their x and y coordinates = 0
and since a rectangle is possible then it a ||gm too and doesnt necessarily be a rhombus and square
is it necessary for sum of their x and y coordinates = 0 for rectangle or parallelogram
diagonals are bisected and of equal magnitude
so if sum isnt 0 then magnitude wont be same of the half diagonals
i dont get your proof
If four vectors add up to zero, that means on rearranging, they form a closed polygon in a cyclic way, so $oz{n}$ vectors can be rearranged to form a quadrilateral with 4 equal sides (rhombus), thus, we have 2 pairs of anti-parallel $oz{n}$ vectors. Now, the antiparallel vectors must cancel each other out so you can see that this must be a rectangle. (Sort of a rigorous way to write it.)
SirLancelotDuLac

wdym by ozn
SirLancelotDuLac

1. ans is parallelogram and rectangle
2. rhombus and rectangle saath mei hona is impossible isnt it?
1. All rectangles are parallelograms.
2. What the rhombus-thing is, is just to prove that for 4 vectors to cancel, the situation will always be like this:
That was not to say that the shape obtained will be a rhombus.
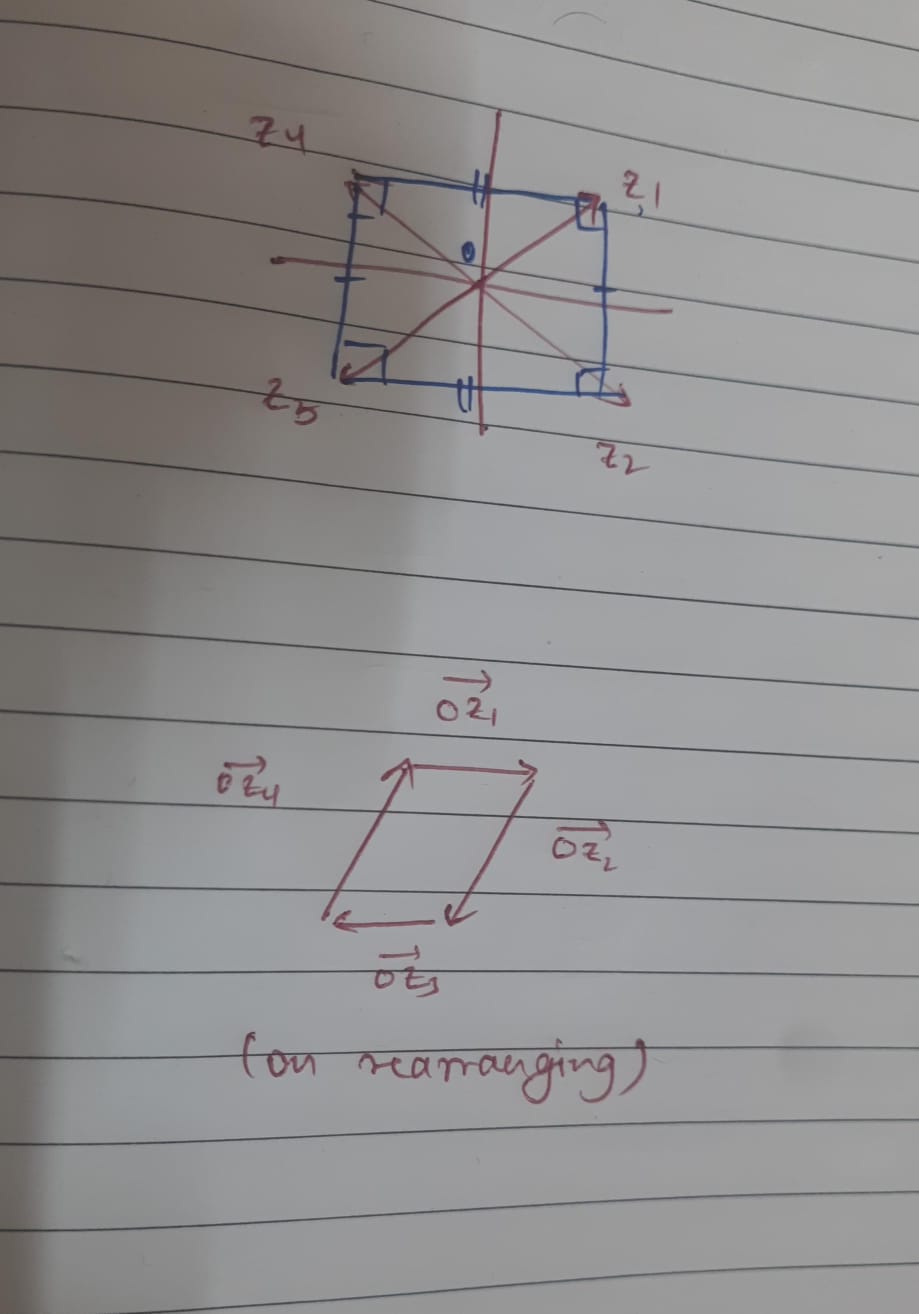
Here, the blue quadrilateral is a rectangle and is your answer. But the red quadrilateral is a rhombus obtained by rearranging the diagonals. (This is just to prove that such a situation cannot exist where there do not exist 2 pairs of anti-parallel vectors in this question.)
ok so from what i undertand is
- it is definetely a parallelogram because 2 pair of parallel lines
- it can become a rectangle
- it cant be a rhombus because |Z| can not be 1 for all points z1 z2 z3 z4
but why cant it be a square , square is just a special rectangle with equal sides but a square is also a rhombus with equal diagonals
It can be a rhombus but that is a special case no?
Visualize that you rotate z4z2 and z1z3 in this figure and you can see that there are variety of rectangle, but a square is a special case.
(Square is a rhombus) but you can also visualize that it will not always be a rhombus.
oh right we are considering only the "must" possibilities
it may or may not be a square but it for sure is a rectangle
cuz square is just special rectangle
and is for sure a parallelogram because rectangle is just special parallelogram
