33 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.its A
i mean is it A
cummute means on multipilcation order doesnt change , LHS they are being multiplied and in RHS they are being added , ORder of A = Order of B if they are addable And that means Order of AB = Order of A = Order of B
Its A,B and C.
oh
Wait order doesn't mean its true tho?
Since that would be true for all square matrices of the same order which is not the case.
(For instance if B=-A, A^2 need not be k.A for some real k)
it is true for all square matrices
all square matrices are cummute
only same order matrices can be added
and AB = some matrix , then there order must also be same
i got A - bI = a|AB^-1|
if u prove AB^-1 = not equal to 0 then its solved
|A/B| = not equal to 0
How do we prove that |A/B|≠0?
i cant think of anything at the moment i will go eat and brb
How so?
ok look Matrix A = nxn (Order)
B = nxn
AB = nxn(Order)
Hence after mutliplying its the same as it was before
i think there might be some missing condition , there isnt any info on A , B Except that they are sq matrix
Order doesn't tell anything tho no?
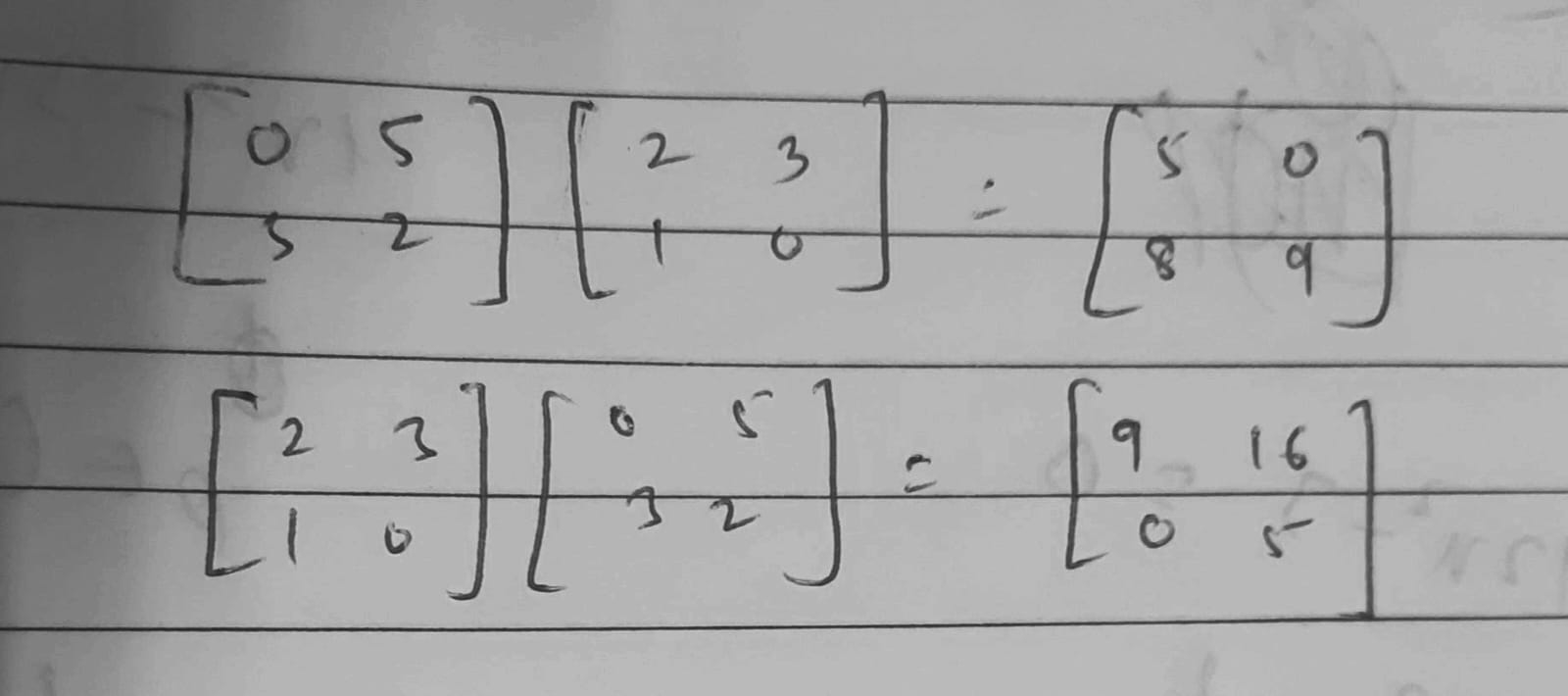
cummute is all about order tho
Here AB≠BA
we talking about order only
not values
AB = BA = A = B
Order only
for commute
@SirLancelotDuLac

AB must be equal to BA which is not always the case
nooo
For instance, this case
Order (AB) = Order (BA)
We talking abt order only
wait
nvm
i get it now
mb
i read it wrong

these silly mistakes are getting out of hand
man wth it seems like there is no info
i will ask my teachers
@SirLancelotDuLac did you get this?
Nope.
The major problem I'm finding here is that we cannot assume A and B are nonsingular
If we can do that, options b and c become trivial
yes
@SirLancelotDuLac @Gamertug asked my teacher and he got b,c.
He said he'll try a as well.
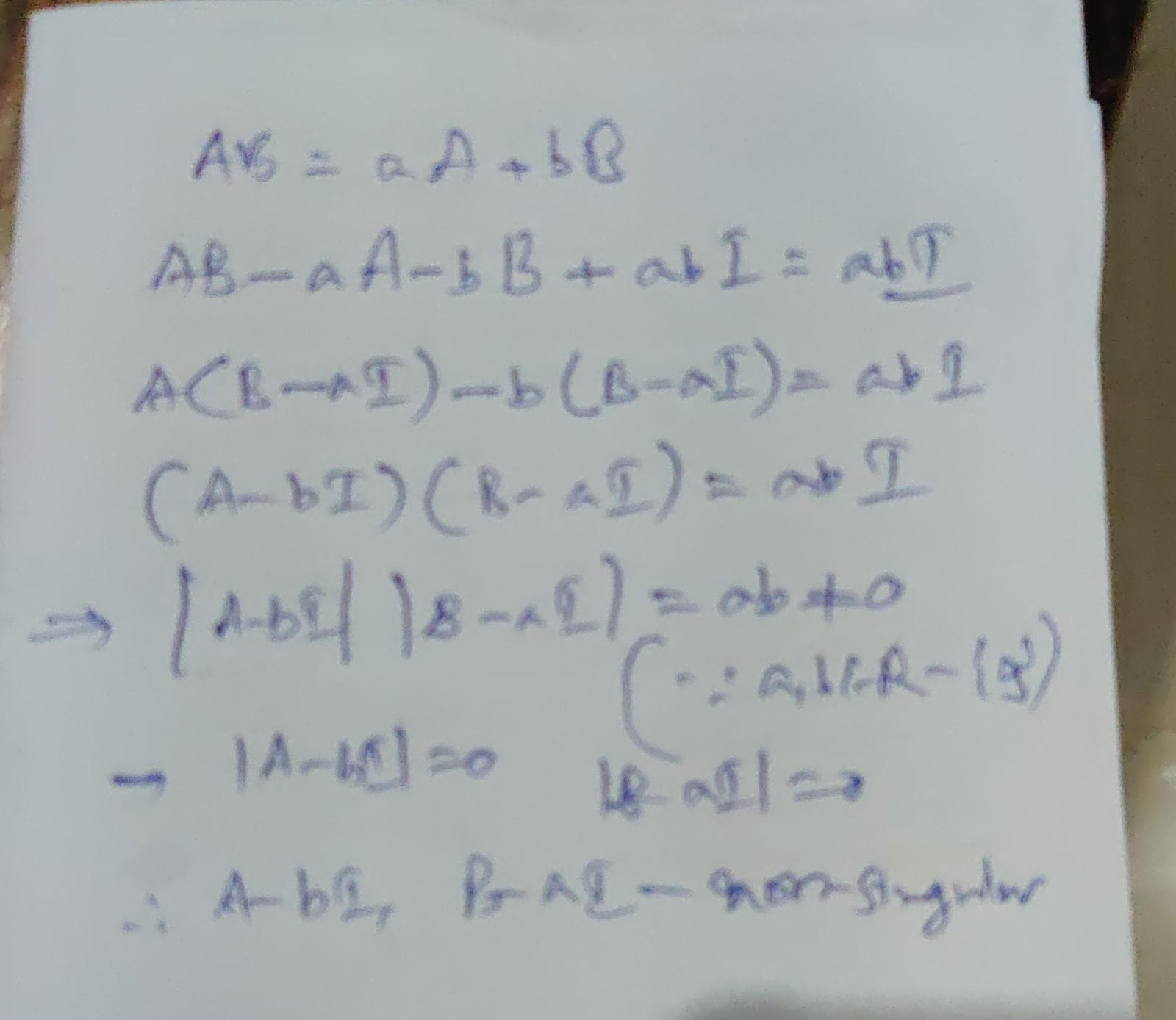
It's embarrassingly simple lol
Ah thanks a lot, mate.
Fr
Oh I got A is well
From this (B-aI)(A-bI)=abI so AB=BA on simplifying.
Because of the order in which you factorise? Yeah, that works out ig
Yeah.
+solved @Opt
Post locked and archived successfully!
Archived by
<@1075951732460376214> (1075951732460376214)
Time
<t:1742303141:R>
Solved by
<@763645886500175892> (763645886500175892)