16 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Write this as sum of $\frac{1}{(a+\omega)(a+\omega^{2})}$ and break this into $\sum(\frac{1}{a+\omega})$ and $\sum(\frac{1}{a+\omega^2})$ Now the first sum is known to us and the second sum is the conjugate of the first sum. (Since $\omega^{2}=\overline{\omega}$ and a,b,c and d are real numbers)
SirLancelotDuLac
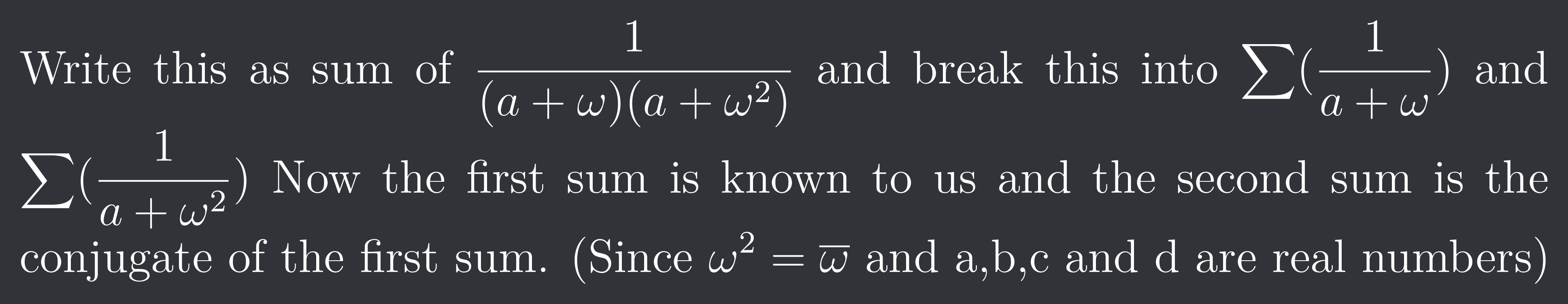
how is 1/a+w = 1/(a+w)(a+w^2)
1/(a^2-a+1) = 1/(a+w)(a+w^2)
$\frac{1}{a^{2}-a+1}=\frac{1}{(a+\omega)(a+\omega^{2})}$
SirLancelotDuLac
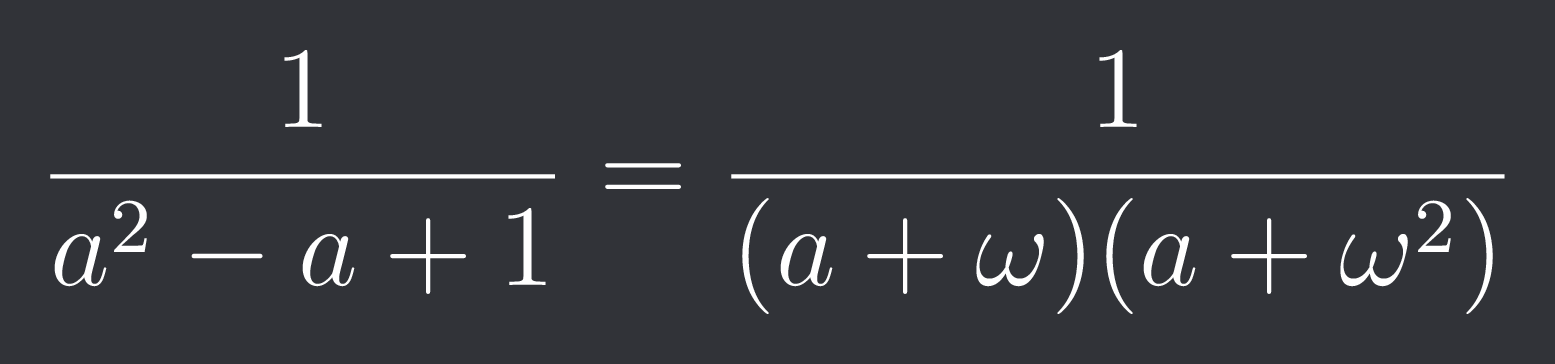

damn how do u even think like that
what the
yeah exactly lmao
@SirLancelotDuLac thought process behind first step? or just standard manipulation
We are given sum of 1/(a+omega) (and given all are reals 1/a+omega^2) so you somehow have to break given expressions into factors of (a+omega) and (a+omega^2)
fair enough
+solved @Prachi @SirLancelotDuLac
we good?
+solved @Prachi @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@1035556259417571408> (1035556259417571408)
Time
<t:1742860312:R>
Solved by
<@926887811674673172> (926887811674673172), <@1075951732460376214> (1075951732460376214)
