36 Replies
@Apu
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Well, a hint would be to sort of think what would be the nature of a function f(k)=$\sum_{r=k^{2}}^{(k+1)^{2}}\frac{1}{\sqrt{r}}$.
SirLancelotDuLac
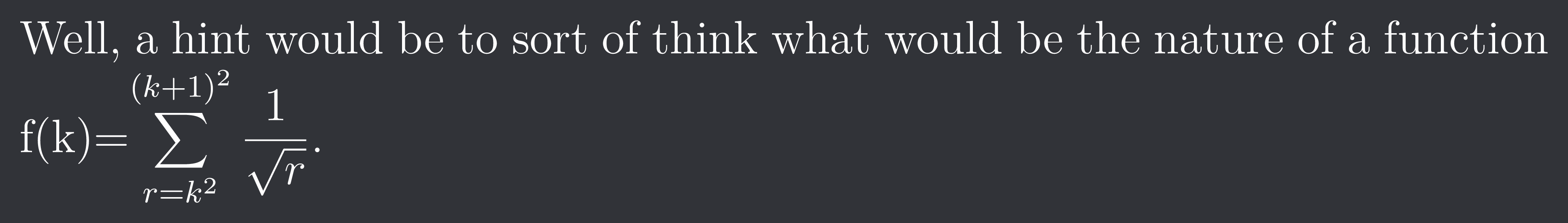
hit and trial mar sakte hai kya?? like n=2
No, like you can see that each term becomes very small so either you can approximate to an integral
Or a more formal solution would be sandwich theorem
sandwich theorem kya hai
Also, don't mind what I send earlier, I miswrote infinity for zero at one place.
Squeeze theorem
In calculus, the squeeze theorem (also known as the sandwich theorem, among other names) is a theorem regarding the limit of a function that is bounded between two other functions.
The squeeze theorem is used in calculus and mathematical analysis, typically to confirm the limit of a function via comparison with two other functions whose limits a...
for 11th or 12th
I'm not sure about that...
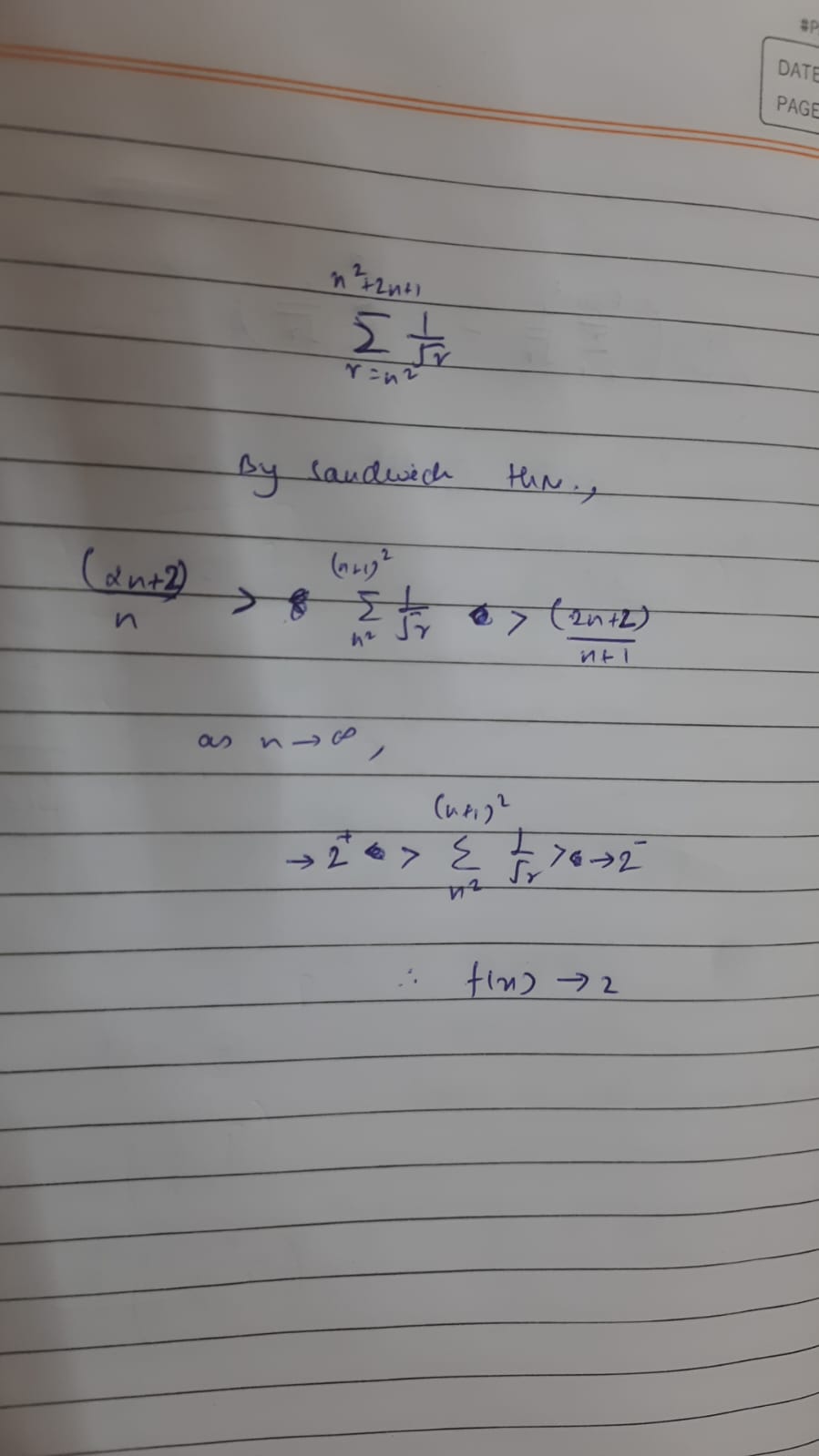
Remember what you did for sinx/x limit proof?
That's sandwich theorem
What would you have as envelope functions?
Isn't envelop sort of "oscillating"?
I meant, for the sandwich. What are the bread slices?
Yeah, that would be as in the solution above. (lower bound is (2n+2)/(n+1) and upper bound is (2n+2)/n) The "term becomes small" thing I used to sort of provide an aliter where you can approximate it as integral.
@Opt hamne bas ratliya prrof kaha dekte
coaching material mai circle se proof kiya hai
Oh wait slight blemmish in the solution (2n+2)/(n+1) is 2 not 2+ my bad
So basically take it as
$\int_{\frac{1}{n+1}}^{\frac{1}{n}}\frac{dx}{\sqrt{x}}$ ?
Opt

i am class 11th student
but yes
samajh sakta hu👍
I totally missed this 🤦♂️
*n^2 to (n+1)^2 ig.
The 1/√ changes it right?
Oh ok ok i see
Got it
Yeah, basically approximating the riemann sum to integral (since each slice is thin)...
Right, I need to get back to comp.sci.
how did u come up with those outer bounds?
Each term is greater than equal to 1/n+1 or less than equal to 1/n and there are 2n+2 terms
i think u said that opp , also i get how it 1/n^2 will be shorter than 1/n but how will 1/(n+1)^2 be greater than 1/n+1
It is 1/sqrt(r), so you wouldn't get 1/n^2?
oh ye mb i get it now
dw bro sandwich theorem is in 12th
how come i didnt think of that when i was solving the paper 😭
why did this retard bot ping twice
+solved @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@1035556259417571408> (1035556259417571408)
Time
<t:1742860297:R>
Solved by
<@1075951732460376214> (1075951732460376214)
