PnC Hit/Trial Alternative
is there a better way to do this other than putting in indivisual values of n1 n2 n3 n4 n5 and tediously finding all 💀

25 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.DUDE I WAS LEGIT ABoUT To PING YOUU
I legit just got out of English exam so don't expect much lol
oh damn
Ok, first just find number of integral solutions using the formula. Then, exclude all solutions where a number is repeated because strict inequality, then, divide by five because we need only the ascending order solutions.
For repeated solutions, the largest one will be 4,4,4,4,4
So you just need to check how many permutations you have with 2 of 1,2,3,4, with 3 of 1,2,3,4 and with 4 of 1,2,3
Tedious but not impossible
That's my method. @SirLancelotDuLac might have a better one.
1. what formula are you talking about 💀
2. DIVIDING BY 5 DUDE THAT IS SO SMART IT DIDNT EVEN CROSS ME THAT IT COULD BE DONE THAT WAY
this didnt make much sense tbh
$\binom{n-r+1}{r+1}$
Opt
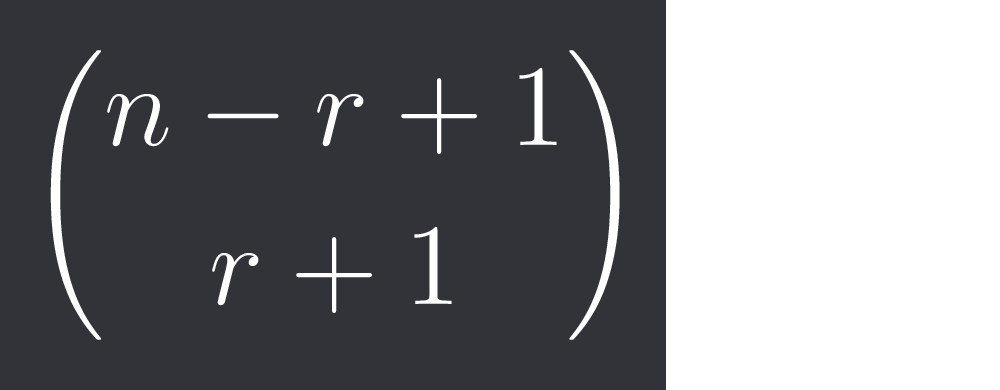
Oops
that was for multiples as far as i remember one sec
Grouping ka formula.
yea i dont think i know that where can i learn that
you just need to find no of unique solutions when n1 n2 ..n5 are not equal and each set of n1 n2 ..n5 will have only 1 way to arrange them.
strict inequality nikalne ke liye we used to add 1 to each number, if i remember right
No that's for non-negative and positive solutions
ohh ok
ok so isko apply kaise karenge idhar
how-
let's take a simpler problem n1+n2+n3 =7 (n1<n2<n3) 1 2 4 is a solution and there is only one way to arrange it such that n1<n2<n3
ok goteem
Unless you know partitions, counting is the only way ig.
Unable to make out more than these I need 2 more

1,2,3,4,10
" " " 5,9
" " " 6,8
1,2,4,5,8
" " " 6,7
1,3,4,5,7
2,3,4,5,6
As far as I could count.
1,2,4,5,8
" " " 6,7
i was missing these two thanks
dude these questions can be 🗿 if you can think of all cases or really leave you 🤡 if you miss cases
anyways
thanks
+solved @hithav @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@964432960197632059> (964432960197632059)
Time
<t:1742222389:R>
Solved by
<@726641475080683522> (726641475080683522), <@1075951732460376214> (1075951732460376214)