17 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.That's $\sum{i} a{i}b_{i}$
Opt
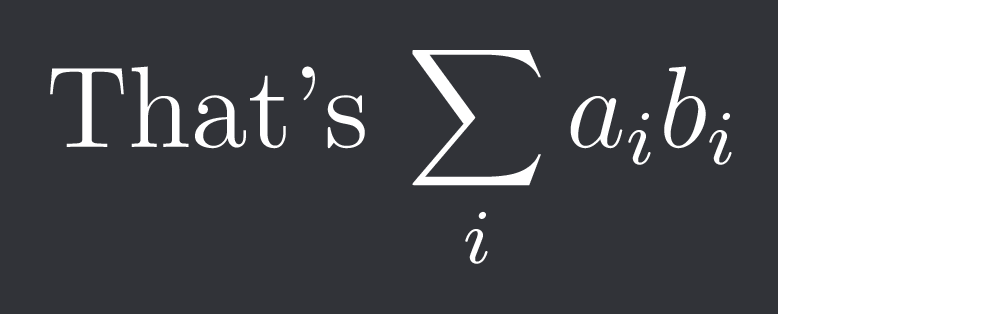
Not a1b1
but ∑a1b1 =a1b1+a2b2+...
btw how it comes?
in what context is this
show the rest of the question/screenshot/wtv
it was basically a proof for cauchy schwarz inequality

What exactly is the doubt?
The proof is something like this let $\vec{a}=x \hat{i}+ y \hat{j}+ z \hat{k}$ and $\vec{b}= a \hat{i}+ b \hat{j}+c \hat{k}$, now $\vec{a}.\vec{b} \leq \abs{a}\abs{b}$, square both sides and replace $\vec{a}.\vec{b}$ by $ax+by+cz$
SirLancelotDuLac
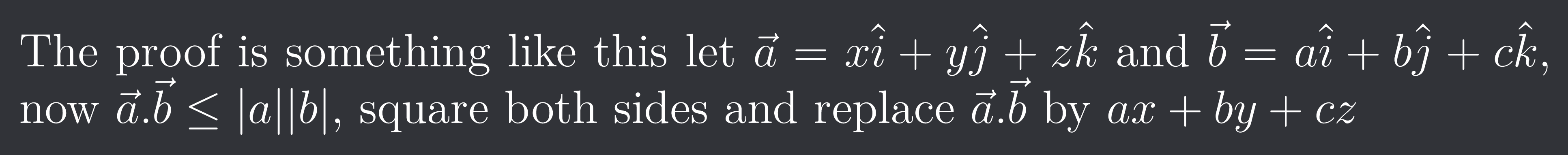
The $\sum{a{i} \cdot b{i}}$ is basically the dot product and nothing else.
SirLancelotDuLac
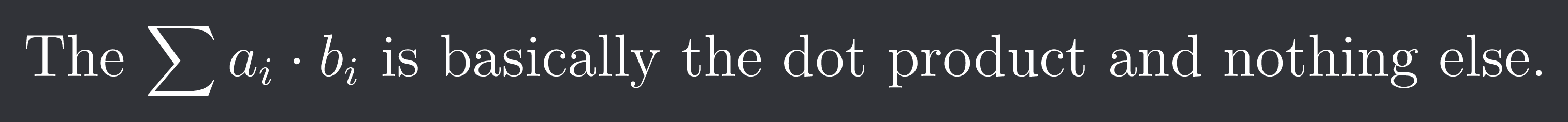
Oh, wait, are you asking why it's product of corresponding terms?
That's the definition of the dot product.
$\vec{a}\cdot\vec{b} \equiv \sum{1 \leq i,j\leq n}a{i}\hat{e{i}} \cdot b{j}\hat{e{j}}$, where $\vec{a}=\sum{i}^{n}a{i}\hat{e{i}}$ and $\vec{b}=\sum{j}^{n}a{j}\hat{e{j}}$
However, since we define $\hat{e{i}}\cdot \hat{e{j}} \equiv 0 \forall i \neq j, and \hat{e{i}}\cdot \hat{e{j}} \equiv 1 \forall i equal to j, $
$\vec{a}\cdot\vec{b} \equiv \sum{1 \leq i \leq n}a{i}b{i}$
Opt
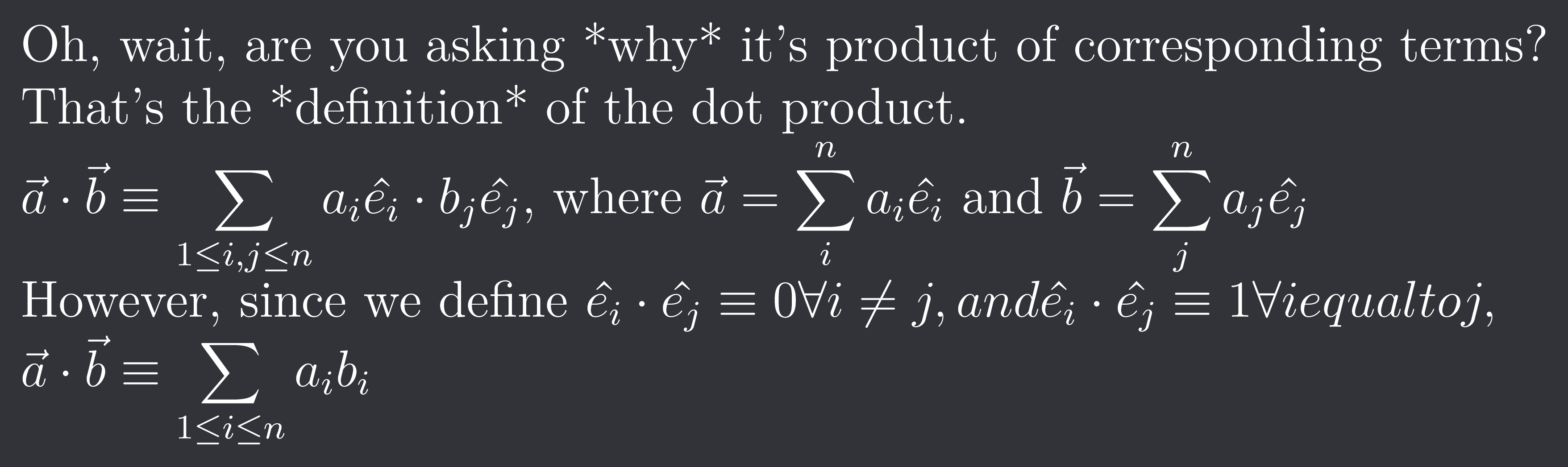
multiplication is repeated addition ahh answer
oh yeah i get it, thanks guys
+solved @SirLancelotDuLac @Opt @BlindSniper (BS)
Post locked and archived successfully!
Archived by
<@1245771182104510557> (1245771182104510557)
Time
<t:1741540896:R>
Solved by
<@1075951732460376214> (1075951732460376214), <@763645886500175892> (763645886500175892), <@418393953742618631> (418393953742618631)
