Integral, trig
$\int_{ }^{ }\frac{\left(\sin x+\cos x\right)}{\sqrt{\sin\left(2x\right)}}$
13 Replies
Nimboi
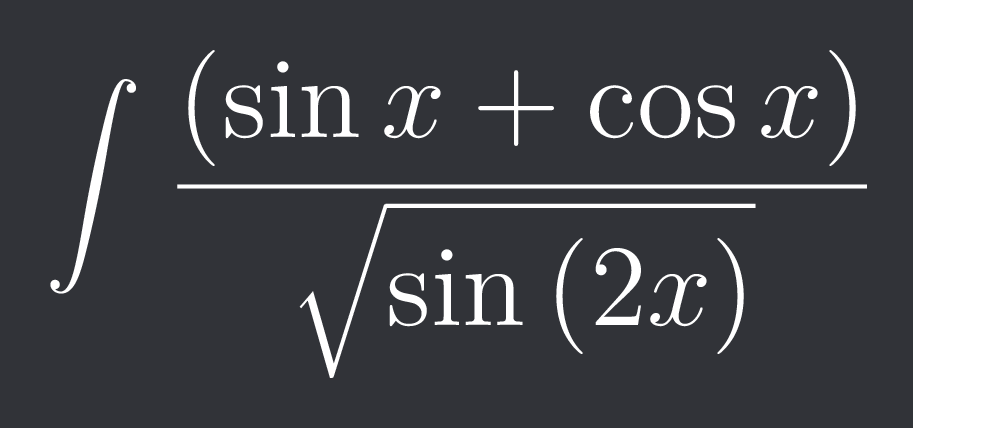
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.splitting the integral and expanding sin2x gives me $\frac{1}{\sqrt{2}}\left[\int_{ }^{ }\sqrt{\tan x}+\sqrt{\cot x}\right]$, which i'm not sure what to do with
Nimboi
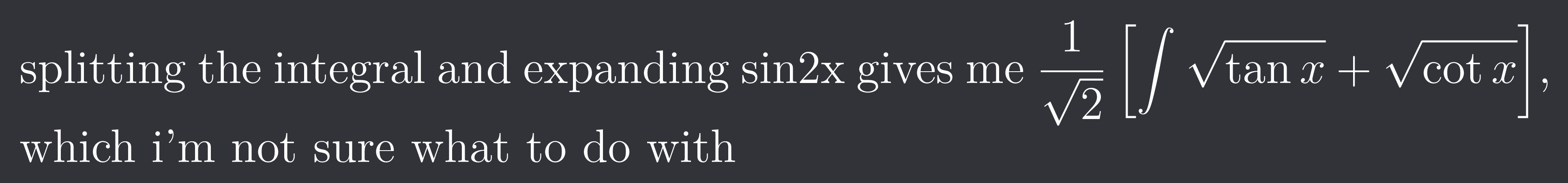
sqrt(cotx) is also in integral, to clarify
Assume sin-cos to be t and then so
*do
sin minus cos?
what's the thought process behind that
it differentiates to give sin + cos but its also not in the integral
oke ill try
Okay, well do try. Also,
1. This is of the form integral of (asinx+bcosx)/f(sin(2x)), where you take integration of numerator as t and eliminate sin(2x) by squaring and stuff
2. Do this here and you get integral of 1/sqrt(1-t^2), which is simple arcsin(t), where t=sin(x)-cos(x)
damn idt i learnt that form
what do you do with the sin2x in the denom
You eliminate it by squaring the t. In this case t^2=1-sin(2x) so you get the value from there.
ahh that's pretty clever
gotcha
is this form a thing you can think of on your own or might i have missed some standard forms i dont know about
eh ill mark as solved
+solved SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@759051317124792351> (759051317124792351)
Time
<t:1741096383:R>
Solved by
<@1075951732460376214> (1075951732460376214)