Radial field due to ring
What and also how to easily derive the radial field due to a ring of radius R at a distance r from the axis of ring, (r<<R)? (slightly outside the ring)
21 Replies
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Inside the ring?
You need to take approximations.
Wait i had this
Oh sorry. Slightly Outside
Wait I think I should share the whole question first.
Yes

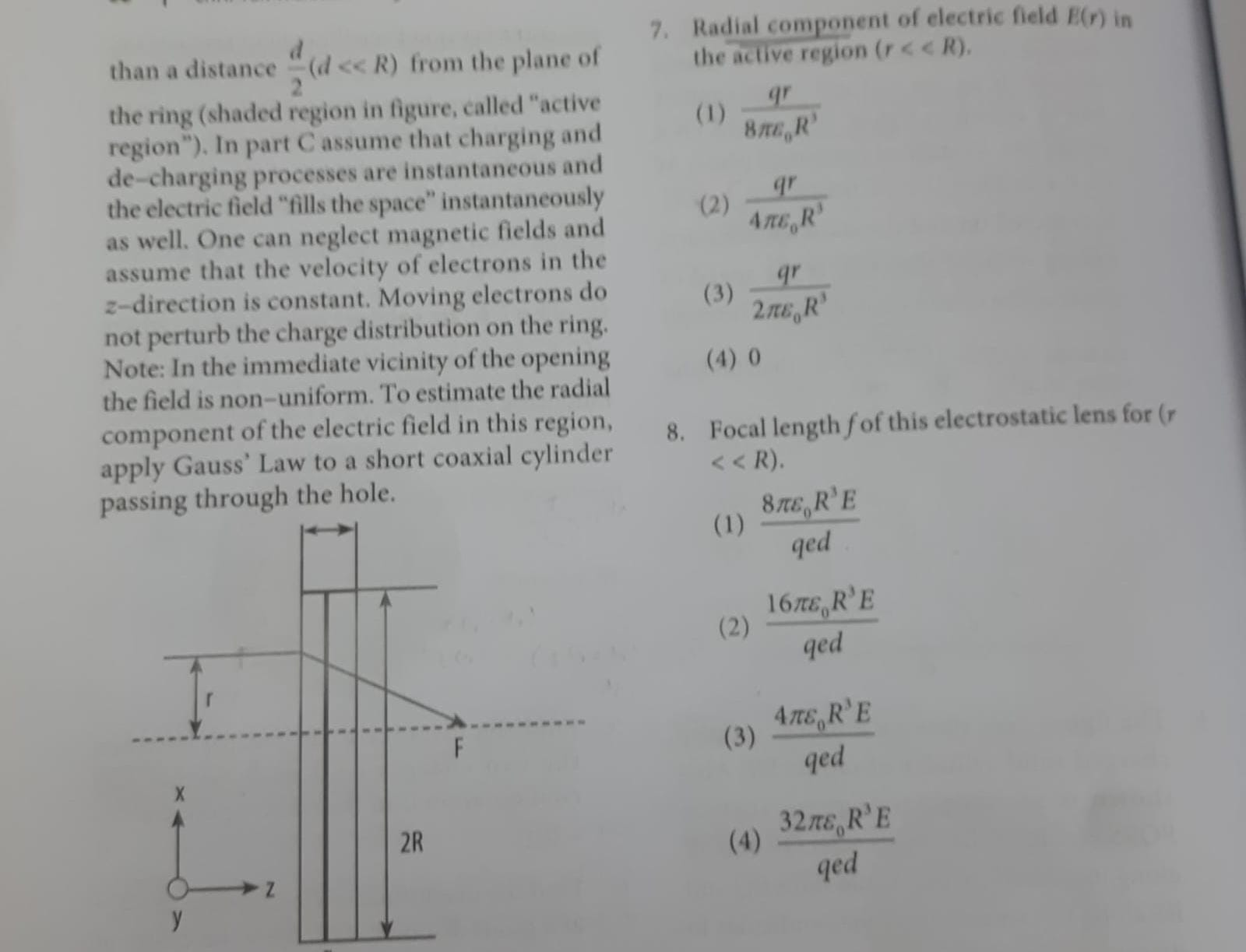
Yep. This is the question. ⬆️
Ok, I think I understood
So basically the field at a point slightly displaced from the axis?
And close to the ring
Am I right?

Ye exactly this situation
I'm not getting a simple answer for this :sweaty:
I couldn't find the apt symmetry condition, so I tried the integral form
And while it's integrable, let's just say it looks very messed up
Let me have breakfast
What's the best Gaussian surface aaaaaaaa
No way, is it zero?
@SirLancelotDuLac
Never mind flux cancels out
Ye that is one of the roadblocks I'm having. No charge gets enclosed in choosing a surface and flux gets cancelled out
Imagine it's a weird Gaussian surface like a torus enclosing the ring
It shouldn't be anything cylindrically symmetric with the circle no?
So as to not let the flux be cancelled ig?
It won't be cancelled if the ring is inside.
You have non-zero flux
Everything is outwards.
Looking at the options, there is no dependence on distance from the plane
Doesn't the radial flux pushing the stuff inside (the portion below a cylinder enclosing the ring itself) compensates the low area with E-field?
Oh no wait Im dumb.
Can you send the full solution once please?
Also, is it safe to assume the radial component doesn't depend on the distance from the ring?
I'm eating rn. Just contemplating
That's my comcern
It's clearly going to depend because inverse square
But for small d, it must be an approximation
@SirLancelotDuLac is it option 2? I did a stupid approximation and got 2
It's (1) according to the answer key.
Screw it I'm gonna try integrating
And of course that doesn't work
It's just too tedious
@SirLancelotDuLac did you try finding field for a point in the plane?
I tbh did not want to assume independancy from d so can't say I have.
But that would be constructive tp the problem yeah.
Apart from the point on the circumference, how would you find the radial field at a point inside the ring?
Ah dude, life hits harder when you realize the question tells you how to do it and yet you skip the paragraph. :sweaty:
+solved @Opt
Post locked and archived successfully!
Archived by
<@1075951732460376214> (1075951732460376214)
Time
<t:1740841220:R>
Solved by
<@763645886500175892> (763645886500175892)