Functions, number of conditional one-one functions
All I've got is that all of the plus terms need to be added to a maximum of 10, so f(a) can only be till 5, f(c) can only be till 3 and f(d) can be till 10.
Also that all the plus terms can't be added up to 1 or 2 in any way since one-one gets violated.
Not sure how to proceed.

35 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.So basically, isn't it asking no.of integral solutions to that equation na?
With distinct integers
And ranges fixed between 0 and 10
sure
yeah it is
what does that do for us
No, maybe framing it differently would help.
Let me get a book brb
Case-working/Systematic conting works here ig
that's a lot of cases to work through
also the answer is 31
That may be true.
Oh yeah systematic counting would work for this no?
I got f(c) is between 0 and 2,
f(a) is between 0 and 4
f(d) is between 0 and 3
By reducing.
This is inclusive btw
Of course, they can't be at the maximum simultaneously, and they can't be equal.
So i think I may have neglected something because this will in no way give 31
how did you reduce it to this ?
same question
It's wrong nvm
alr
i assume for systematic counting to work in a reasonable amount of time we need to reduce further than what i've done?
Ok, I'm applying some number theory here, but we can rewrite the statement as
2a+3c+d = b right?
Oops, I meant functional values at those inputs
yeap
thats how i got my reductions
using that and range 10
Well, the equation will only have integer solutions if b is divisible by the GCD of 2,3, and 1 iirc
oh yeah
Caseworking for f(c)=0
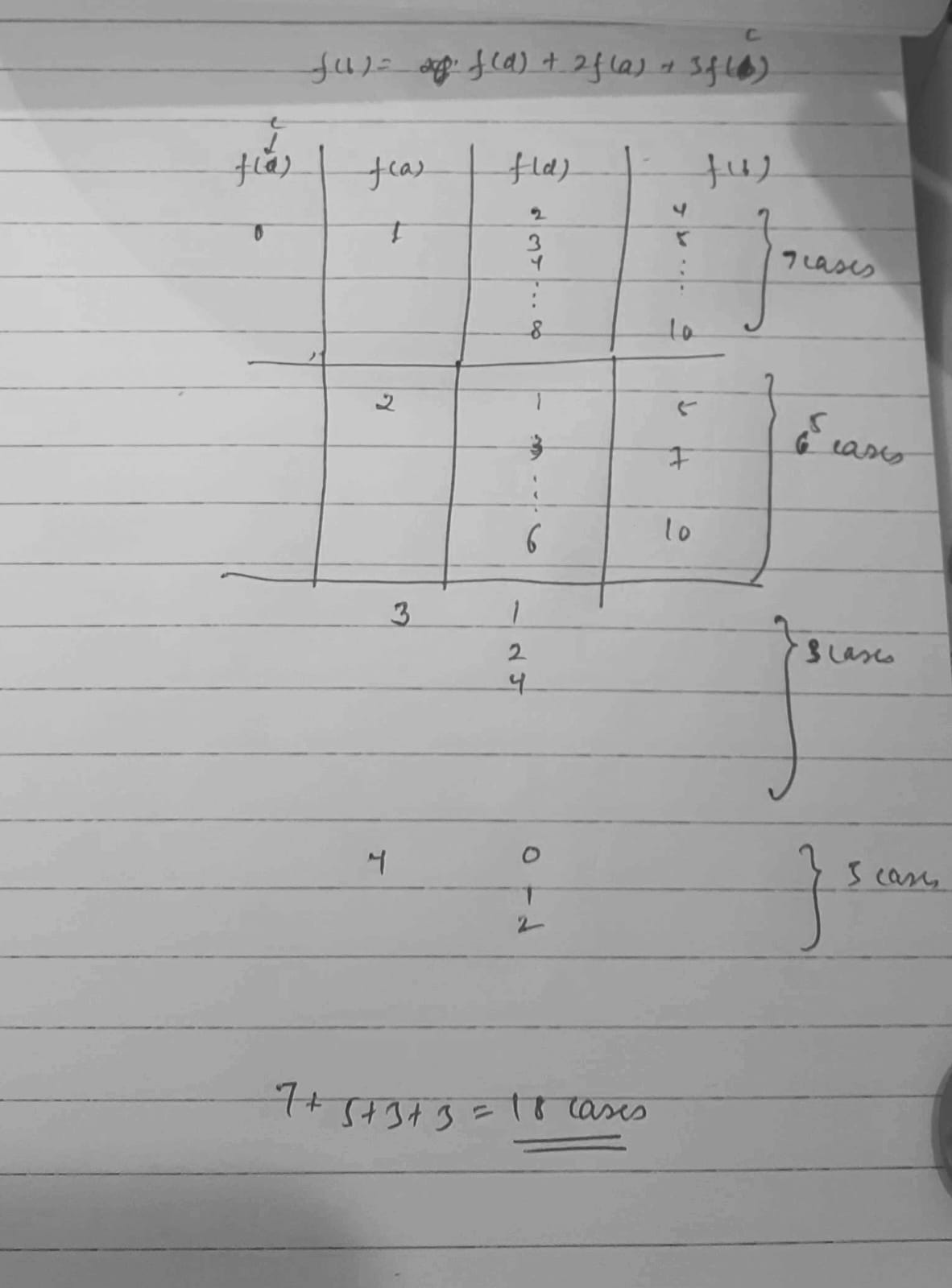
oh that reduces it a lot
Lance, can you verify?
Yeah, this is a question to waste time on, or there's a smart approach we're missing.
Imo number theory won't help because:
1. 1 divides all numbers so doesn't narrow it down
2. "one-to-one" condition makes solutions without case-working difficult.
Oh, yeah, we have a one.
oh right
One-one just means that there's no repeats right?
Yep.
okay yeah, the solution says caseworking
Time waste question?
yeah
definitely
bruh moment
"Mains 2025" aah moment :aah:
this is a 2022 ques 😭 i guess we know where they took inspiration from
Number theory has corrupted me into thinking all questions have elegant solutions.
i too, love getting slapped in the face by the universe not caring about my aesthetic pleasures
Yeah. Physics and elliptic integrals drove that into me.
💀
well, ill mark it as solved then
+solved @Opt @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@717724055217635398> (717724055217635398)
Time
<t:1738251870:R>
Solved by
<@763645886500175892> (763645886500175892), <@1075951732460376214> (1075951732460376214)