S&S
How? I have the solutions but i didn't understand that at all. I tried using the Bell number expansion and subtracting but it didn't work either.
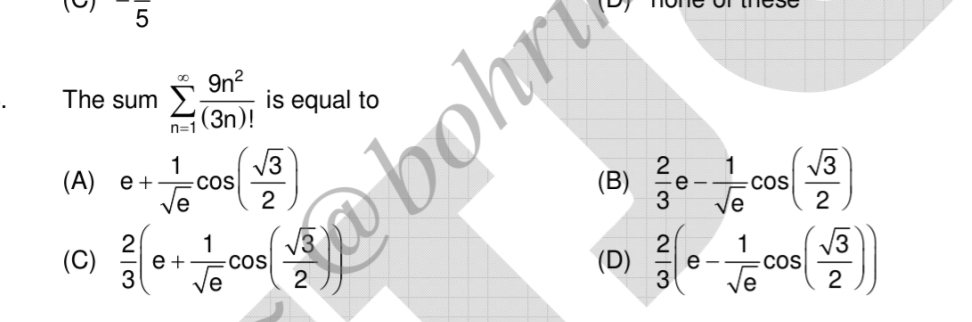
101 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.I have an idea but am not sure if it works.

Ah I see what they did there. When you put x=omega and omega^2, the real part of the power wala portion is -1/2 which you get 2 times so you get 1/sqrt(e) and the imaginary parts are conjugates.
So you get 2/3*cos(sqrt(3)/2)
So answer would be $\frac{2e}{3}-\frac{2cos(\frac{\sqrt{3}}{2})}{3\sqrt{e}}$
SirLancelotDuLac
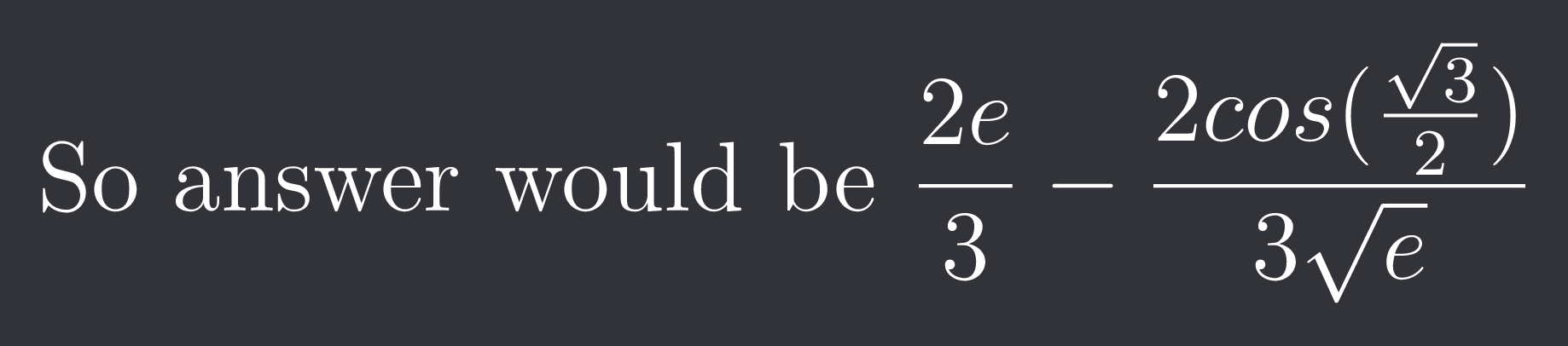
Oh, complex values for x....dammit i forgot that was valid.
I did that for the binomial theorem stuff, but didn't do it here.
This is fiitjee aits right? They're just built different 🗿
Like I would have surely left this in the paper.
Ye lol
I got 180
Nice.
Yeesh, this was a tough one.
And, ik it's not S&S, but I do have another doubt
Sure.
Q53

The (iii) wala toh is true because of I and stuff.
And I have like, zero ideas how to go about proving the first 2.
But the (i) need not be necessary ig.
What?
I don't get it. Why does it have to be 2025?
Oh yeah right.. It doesn't need be.
Answer is C btw. I have no clue why.
There's no solution either. It's too simple for the FIITJEE people to give one
https://en.wikipedia.org/wiki/Idempotent_matrix
It does say that the trace=rank of the matrix
So that does give 2 options.
The only non-singular idempotent matrix is the identity matrix;Nvm
Ah.
Trick question tha
Fr.
But how to prove this tho?
Ah nvm the proof is just multiply by A inverse
Taylor series hai kya syllabus me?
Afaik college first year me hai.



A² = A
Means
(Tr(A)-1)A = |A|I
Now take det on both sides. Should be enough to show |A|= 0 or 1
I mean, it doesnt say explicitly but a lot of questions have comes from it.
And is very useful in cases also.
Advanced me possible hai then. Main me bhi?
Yes.
idempotent is A²=A right?
yes
advanced mein to limits ka sawaal is either taylor series or pure hell
Usually both
mains mein still L hopital works sometimes
Fr
x²⁰²⁵ types in Adv
😭😭😭I hope mains mein aisa kuch na aaye
they like giving exponential on the year we're giving in the exams
mostly binomial mein milta hai ye tho
Ah right and 2025 tends to be a scary number on that part :sweaty:
wait what
45² na
crazy we're living in a square year
last time it was 1936
next gonna be 2116
Yeah that was the trick in the question. non-singular=inverse exists and A^2=A meaning A=I
Goddamn
matrices is Weird like that dude
Kinda midly dislike questions like these where they trick ya by the language
Fr.
Fr
Mujhe to poori algebra iske chalte naa pasand hai ngl
And it's not something you think of checking either, because every question mentions non singular.
Exactly.
Like unless you have seen this thing in writing somewhere your mind doesn't go to it.
ngl i observed in mains 2024 ke papers
the only chapters in algebra that they asked extensively is binomial and sns
PnC Matrices were very less
S&S is one of my faves
they asked 2D alot tho
and fun too
But then you come across questions like this.
2D is my favourite topic in maths
I'm screwed then.
Conics is the bane of my existence
fr
Same 'ere
Entire coordinate was destroyed in 11th ngl.
I've seen that
the people who like Permutations, Algebra jaise topic
tend to hate 2D and 3D
and vice versa too
like i hate algebra with a passion
But now that tangent normal is removed its slightly easier maybe?
last year tha
last year bhi tha
they asked questions still
just mention "line touching the curve at a single point"
Bruh I skipped all that in revision and stuff.
I'm cooked. (Trusted nta for once)
it was pretty basic tho
AoD se bhi hojaayega utna
Fun fact, you know those sums of the type $\Sigma_{n=0} \frac{n^{k}}{n!}$ ?
Those have a general result.
Opt

e^ something wala na?
Well mocks mein I didn't see much tangent and normal wale stuff.
bhai i thought diffraction was removed
Well, no.
Hell nah.
but 2024 mein wave optics se bas diffraction aaya hai
lmao
wahi
Ye, you can differentiate taylor and multiply by x repeatedly maybe?
i revised it again
It's not x^n. It's n^k
K is the external variable here.
Power comes infront of x repeatedly and then you just put x=1
Did this a lot in binomial ig.
yeah integration based series
Yeah, you can do it there, but not here. Because terms end up cancelling up and down.
The only legal method is actually partial fractions iirc.
But if you have k=5, enjoy fifteen rounds of partial fractions.
No wait
More
Wait terms cancel?
Crazy
and how would we do that?
I forgot the LaTex for ∞
What is it again?
\infty
$\Sigma_{n=0}^{\infty} \frac{n^{k}}{n!} = B(k) e$
Opt
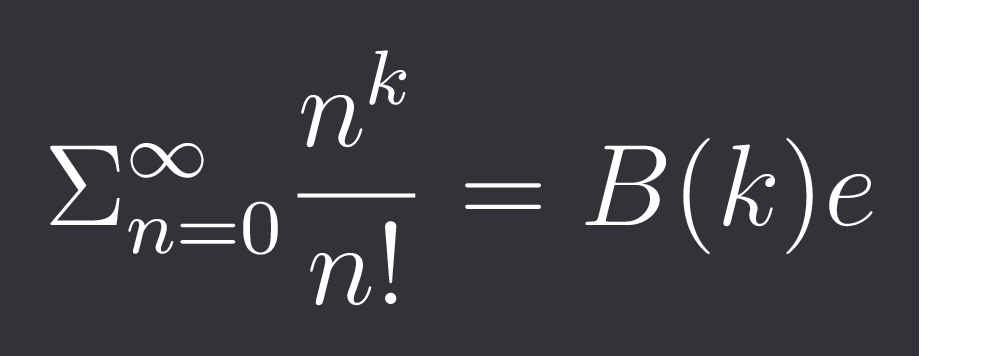
What B
whats
Where B(k) is the k-th Bell number.
Bell number kya hota hai
😭😭😭
Equivalence relations nahi yaad hai kya?
No. Of equivalence relations ke liye ek triangle banate hai na?
Bell's triangle.
wait what
y'all studied relations in that depth?
😭😭😭
i have no clue
I'll have to look it up
You want Relations notes of mine?
🐴 I'll watch a lecture first
uske baad if I'll need I'll ask you
I didn't cover that in relations. Is it relevant for jee?
Adv more.
Not Mains.
For lower powers it works ig
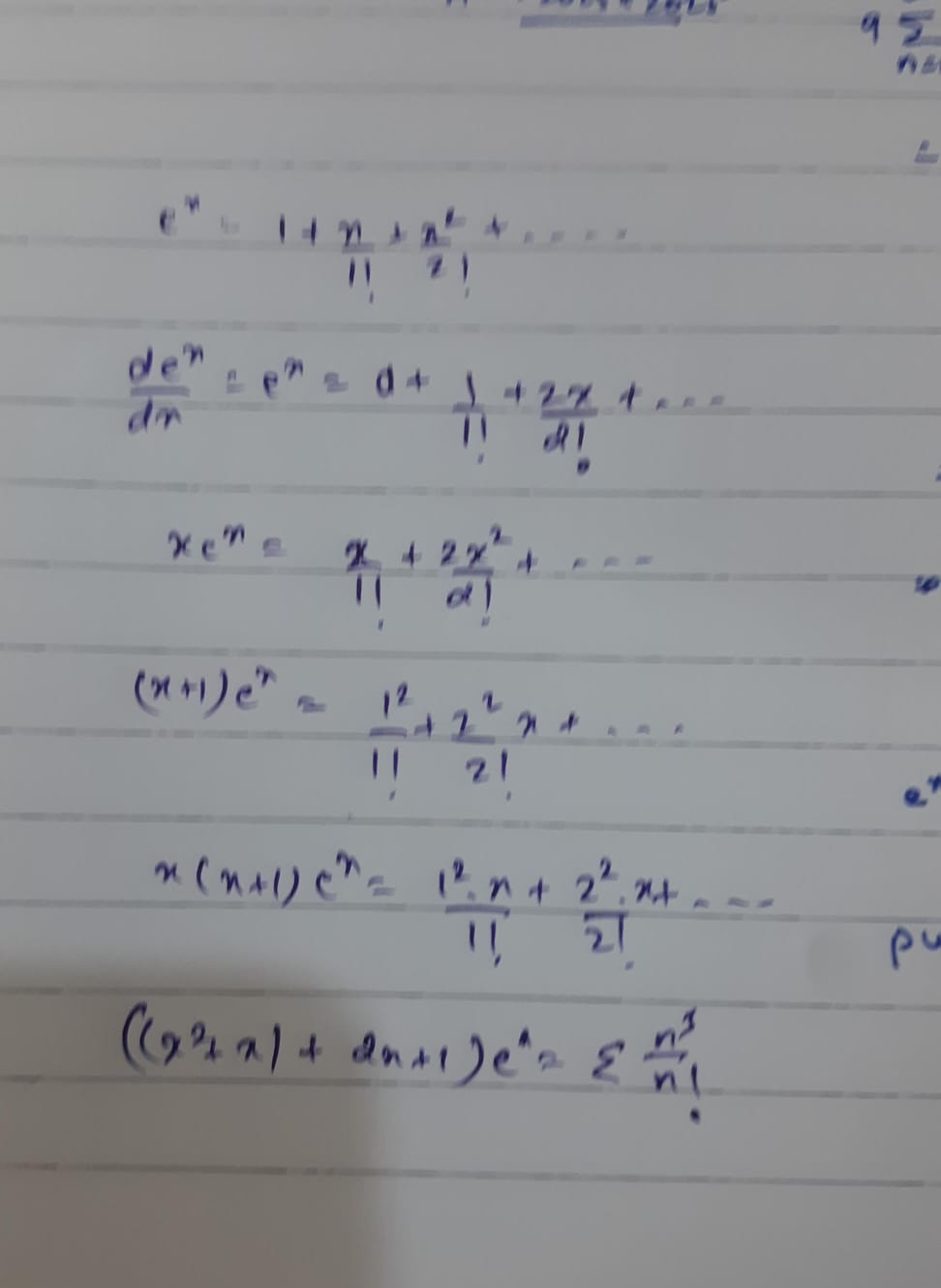
They might ask no.of symmetric and reflexive if anything.
Ah I see.
Nice approach, but what about k=7?
Exactly. Works for lower powers only.
One more not so relevant question.

I'm going through the paper again now.
I evaluated the integral (diff.under the integral) and got I = 1 - cos(1), but I have no clue how to proceed.
Or is this some sandwich theorem based question?
But that was in limits na?
An integral is a limit of a sum.
yeah this correct ngl
0 ke around
sinx/x tends to 1
and 1 pe cos1 hoga
mhm
allen aiot mein bhi to tha ek
sin8x/x wala
wo bhi nahi hua tha merese
🐴
Yeah i messed that one up
Got it later
Just expand and integrate
Taylor expansion se approximation ig?
To how many terms? We have 1800 in the options. I need to go to at least 7! for that denominator
Three terms no? x,x^3 and x^6
Painful neverthless.
Oh right it's sine.
Yeah.
The options all differ by 4/1800
Ya three terms would do it
I think this is good. I'll close the thread
+solved @SirLancelotDuLac @Dexter
Post locked and archived successfully!
Archived by
<@763645886500175892> (763645886500175892)
Time
<t:1737297206:R>
Solved by
<@1075951732460376214> (1075951732460376214), <@1095655769376034818> (1095655769376034818)