32 Replies
The function f(x)=\left|x^2-2 x-3\right| \cdot e^{\left|x^2-12 x+4\right|} is not differentiable at exactly:
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.bot dead
for the quadratic 2 pts
and e^ ke liye 1pt
The function f(x)=\left|x^2-2 x-3\right| \cdot e^{\left|x^2-12 x+4\right|} is not differentiable at exactly:
You haven't used the $$ signs
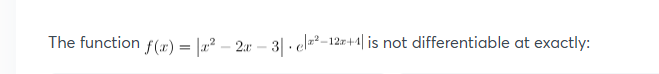
Common roots niklenge I think.
3?
i thought same too
ans is given 2
nahi aaenge
e^ wale ka D -ve hai na
no roots common pretty sure
no
+ve hai
yes
12²-16
oh yeah
+ve
sorry
Yup, just saw that.
😭😭
no no +ve hai
No wait what?
sorry
lol
Hmmmm 2 to aajaenge where x²-2x-3 changes signs
and 1 for e^x
yeah ig
wait a second
wont e^x be always +ve
why we checking for it
Hmmm good point
wait
i am confused
ye ans will be 2
But agar e ke andar wali term -ve hogi then curve ka behaviour change hojaaega na
but since mod hai to it'll always be +ve
sahi baat hai
ig
i hate continuity differentiability man
even if it becomes -ve Curve will be +ve
such an annoying topic
yeah
still not the worst
man function is the worst
Ong
Differential calculus is a pain to study
limits and AoD are still fine
but AoD gets ugly really quickly
ye
+solved @Dexter @Opt
Post locked and archived successfully!
Archived by
<@700658749416669194> (700658749416669194)
Time
<t:1737184777:R>
Solved by
<@1095655769376034818> (1095655769376034818), <@763645886500175892> (763645886500175892)