17 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Well ig there would be 2 cases:
1. Denominator has 2 distinct roots
2. Denominator has one root and numerstor changes sign at that root.
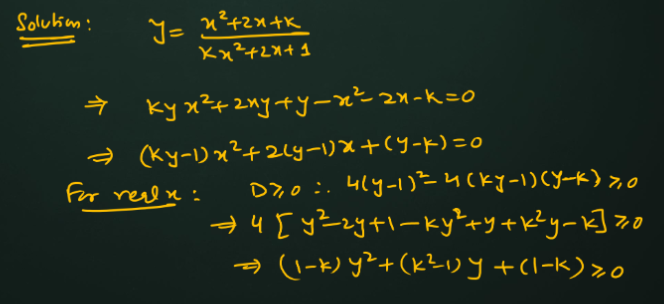
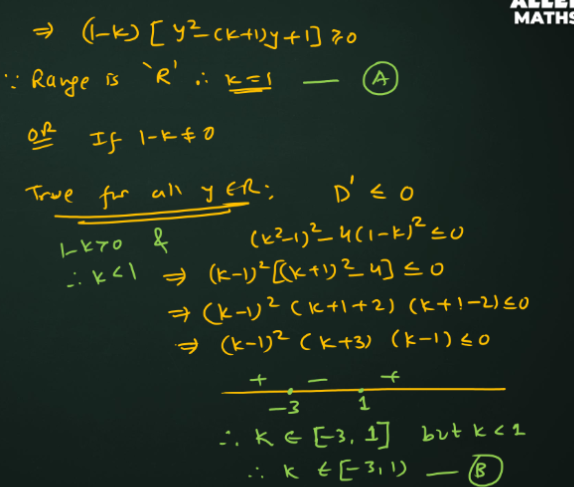
why is D' less than equal to zero ?
not greater than equal to ?
for y to be real
Oh right. But why the above works is because for x to tend to + and - infinity both denominator must tend zero when the numerator is both positive and negative
Denominator is never 0 thereforce discriminant < 0 so it will never be = 0.
Ahh diff approach
didn't understand
you can do D > 0
right ?
D is not eqaul to zero
Range Belongs to R honi chahiye
D less than zero isiliye kiya hai because y² - k+1y +1 wali term should always be positive for the range to be real
it just means ki K se independent rahega Maamla
The range would be R when this equation ka discriminant is Greater than zero for all X belongs to R
oh is d < 0 pe positive hota hai ?
Agar square wali term ka coefficient > 0
and D< 0
then the quadratic is positive for all X
like x²+x+4
iska graph banaoge to it'll always be above x axis
isme x² ka coeff > 0 hai and D<0
The best method is as Dexter explained but ig this should also work: The expression takes all values toh it must assume +infinity and -infinity (not literally, basically must tend to both these values) somewhere. Iska matlab denominator must be going to zero somewhere. Now jahan pe denominator zero ho raha hai un value(s) ke neighbourhood mein numerator/denominator ko +ve aur -ve dono hona chahiye. Building on this may work ig
This is a standard question
+solved @SirLancelotDuLac @Dexter
Post locked and archived successfully!
Archived by
<@754965160803696670> (754965160803696670)
Time
<t:1737364819:R>
Solved by
<@1075951732460376214> (1075951732460376214), <@1095655769376034818> (1095655769376034818)
:]
