Limits
Let's see if I remember how to type this out.
$\lim_{x \to 0}\frac{cos(sinx)-cosx}{x^4}$
I tried series expansion, and got somewhere, but it didn't work out in the end.
38 Replies
Opt

@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Series expansion works na?
In this?
Just make sure you use sine ka series expansion also.
Like $(x-\frac{x^{3}}{6})=sin(x)$ le ke sine and cosine ka series expansion
SirLancelotDuLac
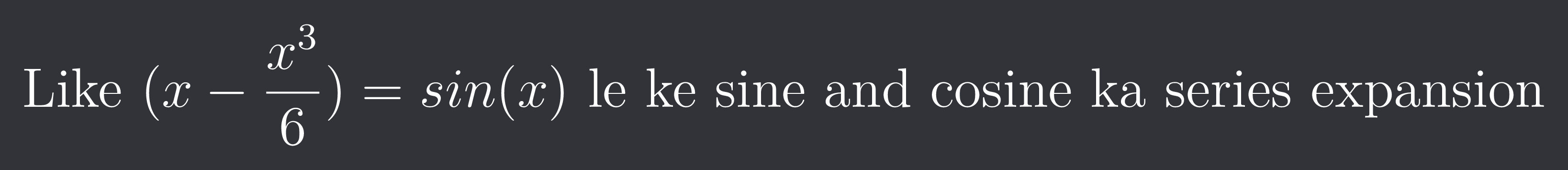
you're suggesting series expansion of sin inside a cos and then series expanding that expansion in the argument of cos?
Oh, I just expanded the cosines
That would ignore several x^4 terms that come by sine wala lagane mein ig.
I have the question in my module 😆😆😆
Yeah, I got those zeroes in the denominator and went nah
First expand by cosine and then apply sine in my opinion.
Achcha so like we first assume like sinx to just not exist in the cos, write the cos ka expansion and then put sinx everywhere where it should
Ye
I guess that should work
Ye and then apply sine ka expansion.
Even after that its still painful tho.
AYEIN
NAHH ATP JUST SKIP THE QUESTION 😭😭
It is. Three terms at least in each expansion, because x⁴ in denom
That's what I did lol.
Yeah. In paper just have a hindsight what to ignore ig.
And four mistakes. So 76 in maths today
not that difficult tho
send paper
I will.
I made silly errors lol
76 is pretty wild
It was easy
I'll judge
2/3 @Opt ?
no 1/3 sorry
eh?
1/6 diya hai
naw wait
It's in that paper I just sent
oh it actually is pretty easy
damn
yeah 1,-1 krna hai bas
was talking about the paper
oh
sorry
😭
got it
lemme send the soln
Ok, yeah, I think I got this.
@Opt sorry for the mess
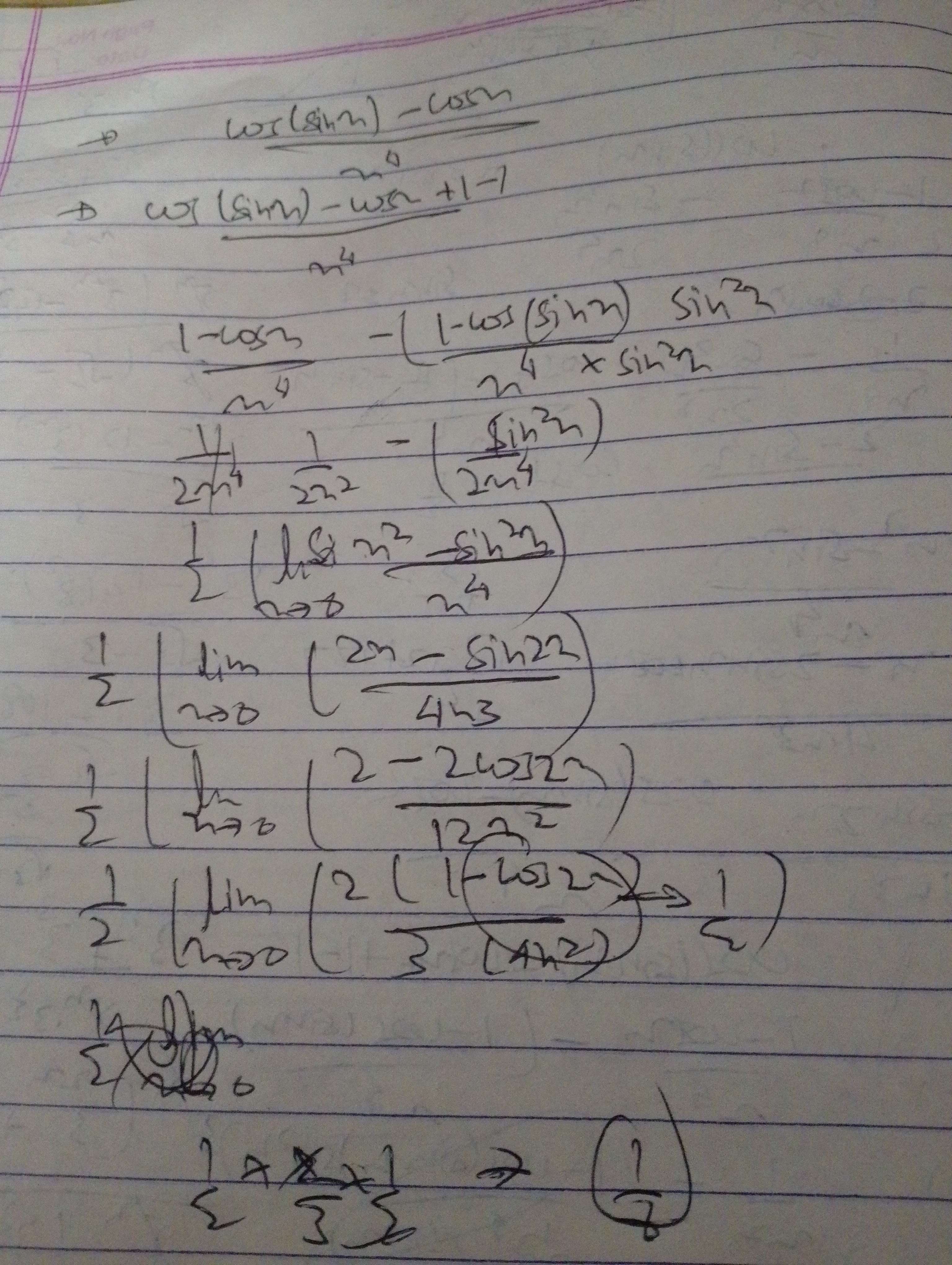
just standard limits and L hopital
Understood. Series expansion worked out for me.
good stuff man
Aight, imma close this.
+solved @Dexter @BlindSniper (BS) @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@763645886500175892> (763645886500175892)
Time
<t:1736946639:R>
Solved by
<@1095655769376034818> (1095655769376034818), <@418393953742618631> (418393953742618631), <@1075951732460376214> (1075951732460376214)