gravitation
a satellite goes along an elliptical path around the earth the rate of change of arc length a swept by the satellite is proportional to r^x . determine x
44 Replies
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.you want derivation?
its kepler's law tho
its arc length not area
i dont recall which law of kepler had arc length
whats the area swept law tell crow?
in equal time equal area is swept
dA/dt = L/2m
whats dA here
tell crow
infinitesmally small area
dA = 1/2 r^2 d(theta)
agree?
wasnt it dt instead of dtheta
ara bhai
area of a sector
areal velocity= mvr/2m=vr/2=root (Gm/r)*r
rate of change of area is proportional to r^1/2
i understand this of second law
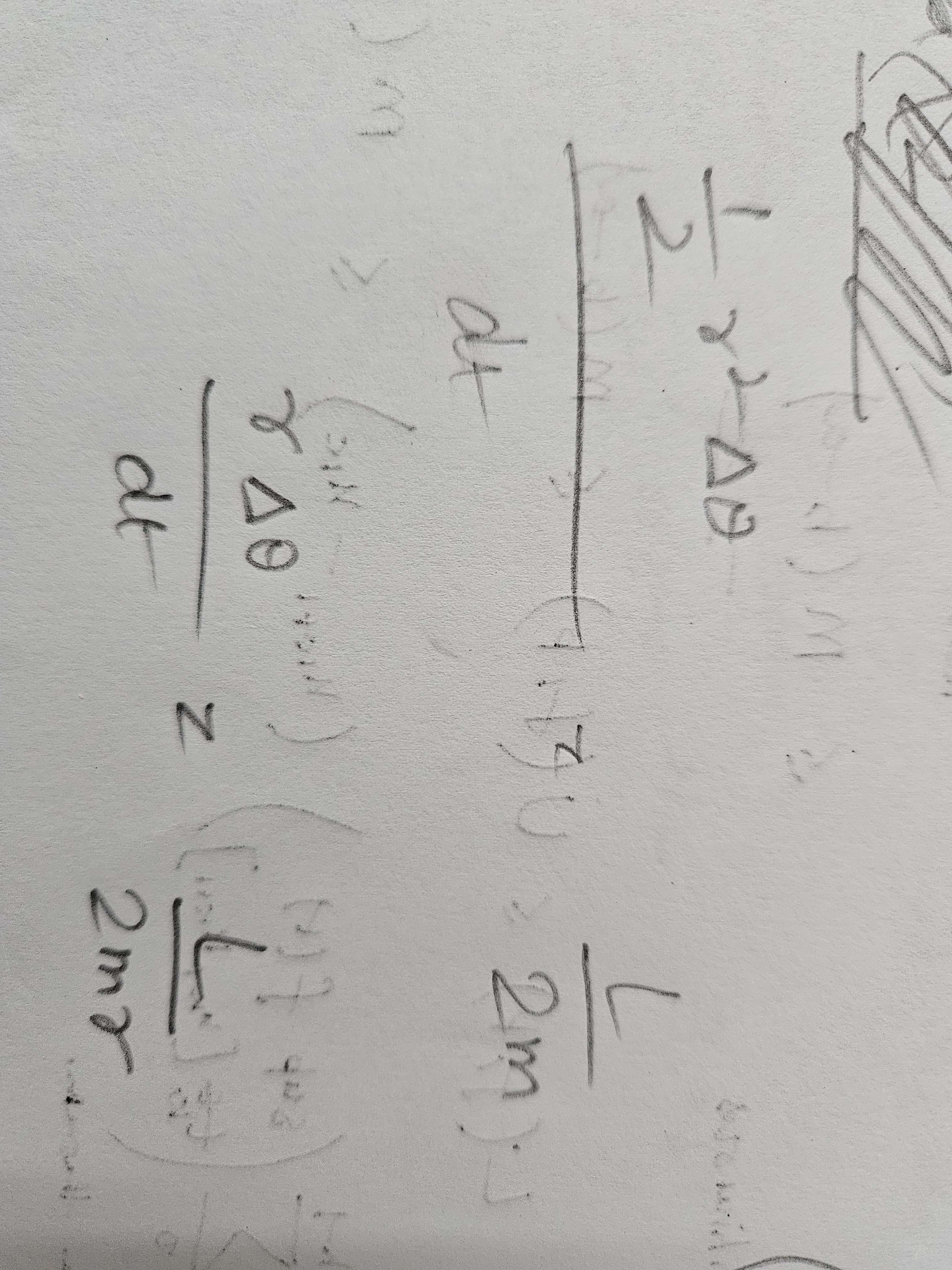
Evaluate the right side in term of r
@hardcoreisdead clear?
OHHH
got it
thanx
so i basically had to write area in terms of r and dtheta
and derive relation between
Mhm
can u solve another one
a uniform ring of mass m and radius a is placed directly above a uniform spehere of mass M and of equal radius. the centre of the rings is at a dist (root3)a from the centre of the sphere. find the gravitational force on the sphere by the ring and vice versa. are they both equal? is so why?
@SIMPle Potato
or should i create new thread
In end it will mr not 2mr
Yea dosent matter tho we only care about r
1/2 will cancel it out
Mhm
You know about gravitational field due to ring?
on axis?
yes
Yeah
Just like electrostatics assume sphere to be a point when considering other ones field
for the case of gravitational force due to ring on sphere
right?
So its F = (field due to ring at center)*mass of sphere
Yeah
Force is same for other case cus of newton's third law
ignoring newtons third law for once
how can we mathematically find out the gravitational force on ring due to sphere
thru calculus
do we have to assume sphere as point mass here
if yes then its just derivation of g-field on axis
Yes
It would be at some angle one component will cancel its counterpart you'll have to integrate the other one
if this is system then particle mass must be at axis right
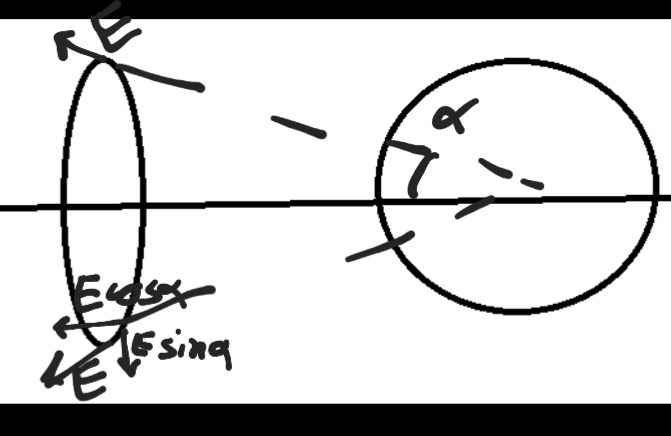
Sin component will cancel
yeah thats clear
will this be completely accurate tho
assuming the sphere as point mass
cuz the mass at top of sphere will experience more force than the mass at few units below it
No?
Asumming it to be point mass would create no problem
i meant looking at an actual sphere
not point mass
dosent matter try solving with that assumption
whi toh ni hua
too many variables

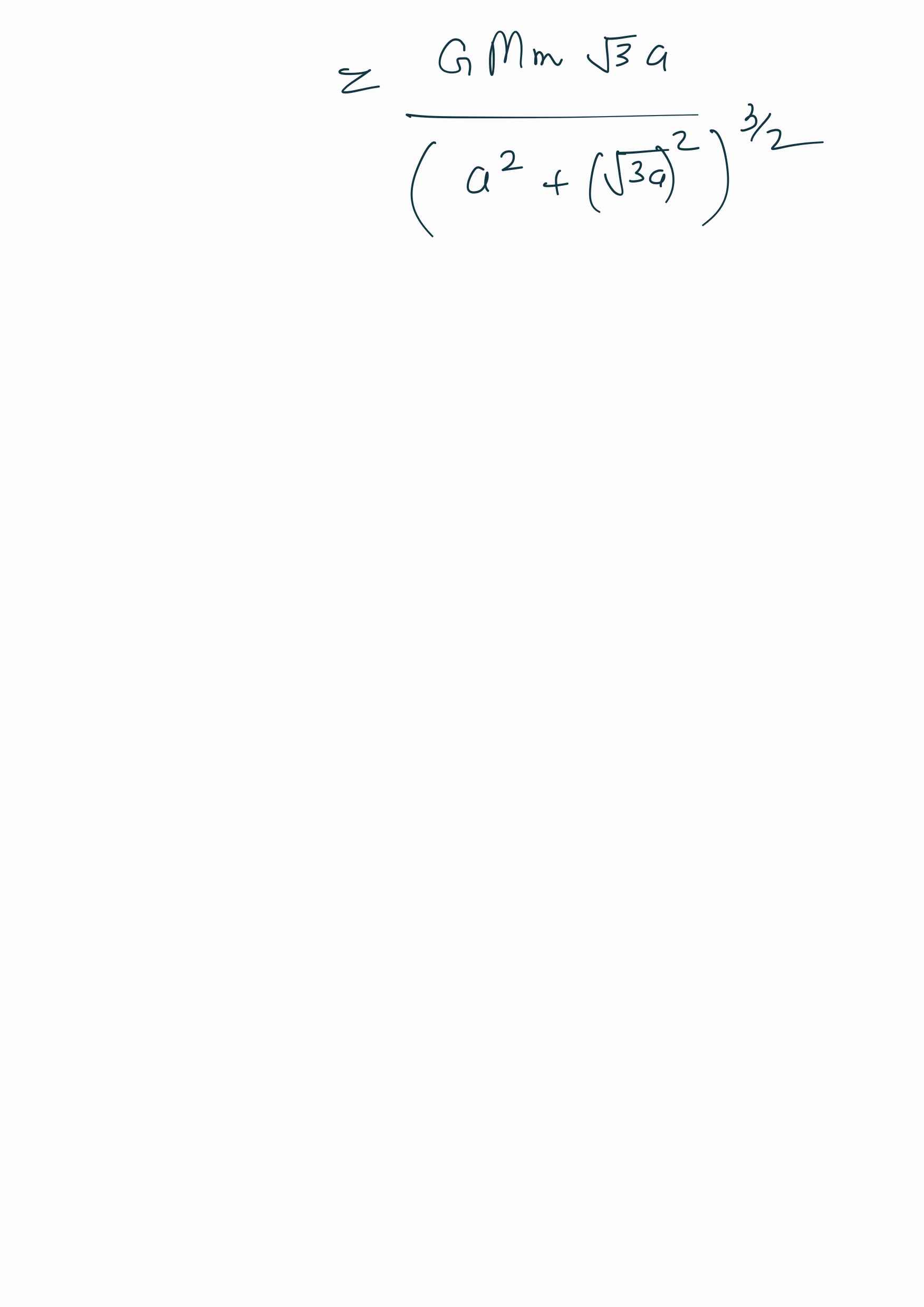
@hardcoreisdead
this portrays gravitational force due to dm mass of ring
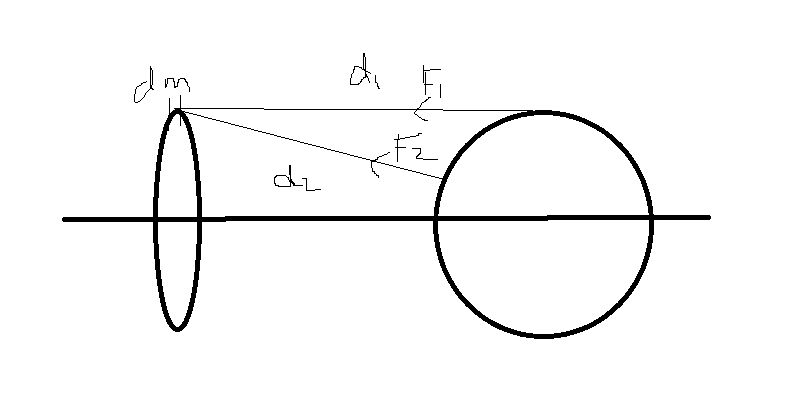
on some mass m of sphere of total mass M
F1= Gmdm/d1^2
F2= Gmdm/d2^2
d1>d2
F1<F2
in real life wouldnt this create discrepancies
dude make new posts please. and also thanks @SIMPle Potato you are awesome.
I am closing this one out :D
+solved @SIMPle Potato
Post locked and archived successfully!
Archived by
<@1035556259417571408> (1035556259417571408)
Time
<t:1730948834:R>
Solved by
<@813788193286914068> (813788193286914068)