Rotation
Why can we not do this while energy conservation?
mgh = 1/2 mv² and the put v = rω
doing mgh = 1/2 Iω² gives the right ans (15)

11 Replies
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.r is distance btw pivot and com
its energy conservation only?
Yes, only energy consv gives the ans, but with Iω²
Iω²/2 is the same as 1/2 mv2...u just put v=rω
its like the rotational kinetic energy for the whole rod
and the rod is only rotating and not translating about the pivo
t
So 1/2 mv² isn't valid here?
You can't write kinetic energy of a rotating body only using com, it requires mass distribution too. When putting v = rw, you're ignoring mass distribution
1/2 mv² is still valid but you have to integrate
1/2 Iω² comes from integrating 1/2 mv² since an extended body has infinite particles...we just add all their 1/2 mv² where v is rω since the particles are rotating (i.e. circlular motion)....also since ω is a constant for each particle in rotation its treated as a constant when ur summing the kinetic energies.
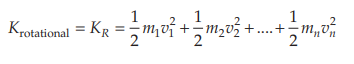
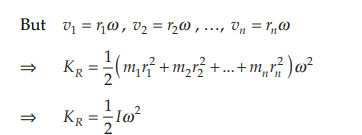
Ahh thanks so much
+solved @_masterchef @Ace007
Post locked and archived successfully!
Archived by
<@1275829425933385788> (1275829425933385788)
Time
<t:1730600981:R>
Solved by
<@1073259689694994442> (1073259689694994442), <@1049664259845521479> (1049664259845521479)