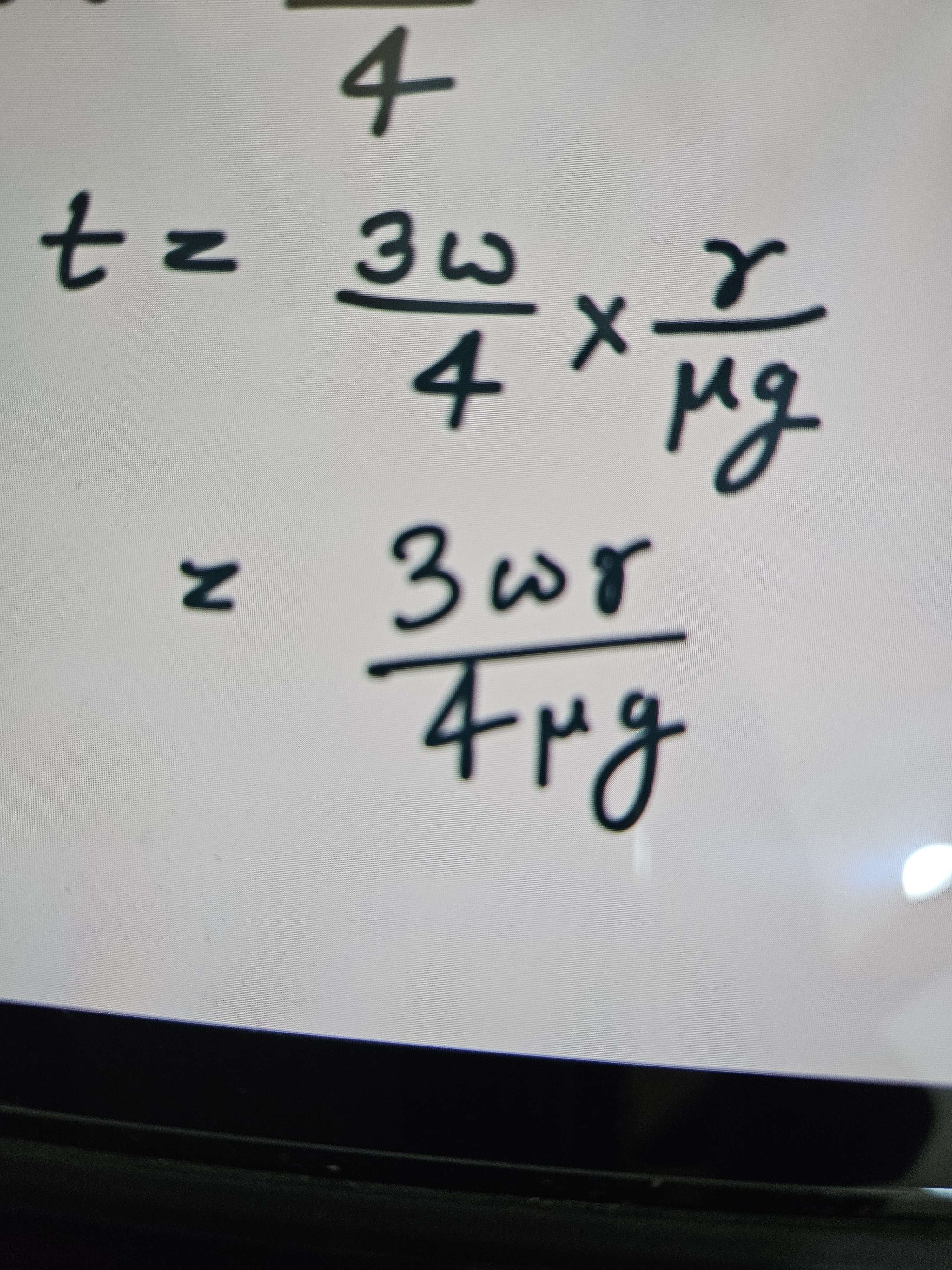rotational
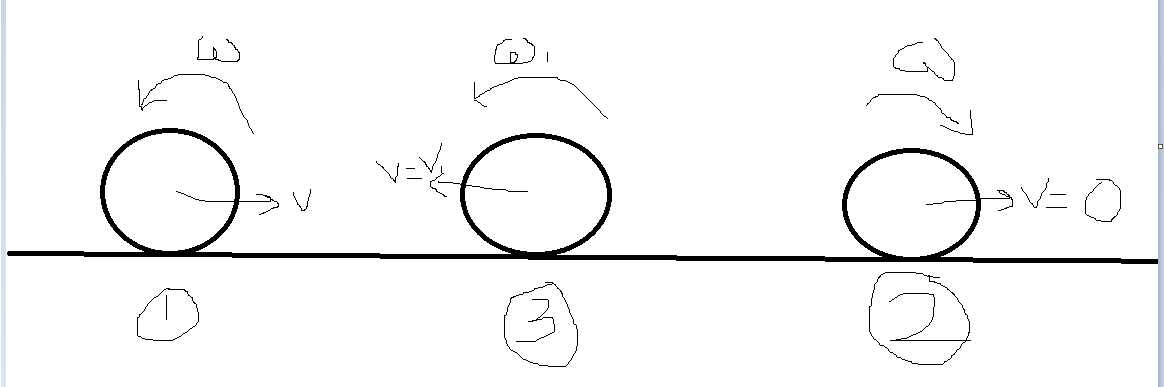
A disc of mass m radius r is given a velocity v and angular velocity w and released on a horizontal surface with coeff of friction u. It is given that v=rw/4 and w is opposite to v then find time at which pure rolling starts.
14 Replies
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.acc to me torque is zero at the point of contact of disc with surface so angular momentum can be conserved . i got L initial as mvr kcap and L final as 3/2mr^2w1 kcap where w1 is angular vel after reaching pure rolling
i finally get w/6=w1
or 2v/3 = v1
Find the time at which speed of point in contact with ground is zero
in order to achieve pure rolling w must switch its dirn right? so here , before that happens v becomes 0 somehow after that disc starts to move backwards. i cant figure out how do we know v becomes 0
kind of like this
Yes
L initial ko dekh ke how do we know this particular case happens
According to me the friction will decrease the angular velocity w to w/4 at some point in time which will be equal to velocity of com and then velocity of point touching the ground would be zero
I could be wrong im not that good at rotation
@hardcoreisdead is this answer
i am not sure but i got the explanation of changing of dirns
and L initial and final are in same dirn and for pure rolling they must be in same flow. for this dirn of v must change
we good?
yeah
+solved @SIMPle Potato
Post locked and archived successfully!
Archived by
<@741159941934415883> (741159941934415883)
Time
<t:1730957710:R>
Solved by
<@813788193286914068> (813788193286914068)