Definite Integration Doubt
Consider the function f(x)=$\int_{0}^{x}{(x-t)^{2}g(t)}dt$ Given the value of g(1) and integral of g(x) from x=0 to 1, we are supposed to f''(x)-f'''(x)
8 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.SirLancelotDuLac
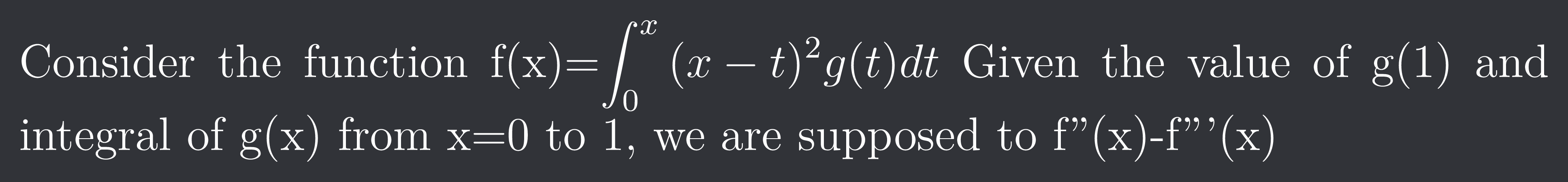
I understood the solution, but is there any other (more generalized) way to find derivative of $\int{0}^{x}{f(x,t)}dt$ without resolving into into $\int{0}^{x}{f(t)}dt*g(x)$
SirLancelotDuLac

you can use leibniz rule in its original form directly but it would just become too complicated.separating function would be a better way to avoid wierd calculations.
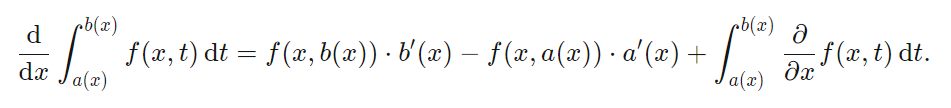
Oh yeah, I see.
Thanks a lot mate.
+solved @hithav
Post locked and archived successfully!
Archived by
<@1075951732460376214> (1075951732460376214)
Time
<t:1728737015:R>
Solved by
<@726641475080683522> (726641475080683522)