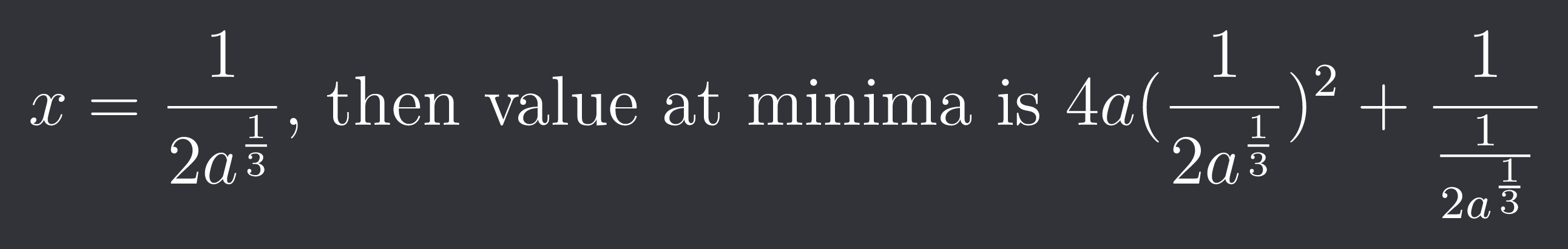Search
Star
Feedback
Setup for Free
© 2026 Hedgehog Software, LLC
Twitter
GitHub
Discord
System
Light
Dark
More
Communities
Docs
About
Terms
Privacy
application of derivatives (maxima minima) - iTeachChem
i
iTeachChem
•
2y ago
•
20 replies
bingbong
application of derivatives (maxima minima)
Asked to find the least value of a
€R for which 4ax
²
+1
/x
≥1
, for all x
>0
iTeachChem
Join
A Study Community for Everyone and Everything. We have weekly sessions on Spirituality, Math and Science! JEE, NEET prep? All doubts are crowdsourced. Hare Krishna!
1,690
Members
View on Discord
Resources
ModelContextProtocol
ModelContextProtocol
MCP Server
Similar Threads
Was this page helpful?
Yes
No
Similar Threads
maxima minima
i
iTeachChem / 💭│doubts
2y ago
Maxima and minima ques
i
iTeachChem / 💭│doubts
9mo ago
AOD maxima minima pyq
i
iTeachChem / 💭│doubts
2y ago
Application of Derivatives doubt
i
iTeachChem / 💭│doubts
2y ago
