11 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Draw figure and use the fact that tangent is perpendicular to radius.
Then diameter of the circumcircle of PBA is line joining P and common center.
So locus is also a circle with radius half of the outer circle I think
plot , obtain coc from 50,114.1 , determine intersection points of coc with c2
now u have three points so find eqn of circle and determine the values being asked
ik my approach is quite big, trying to think of a smaller one
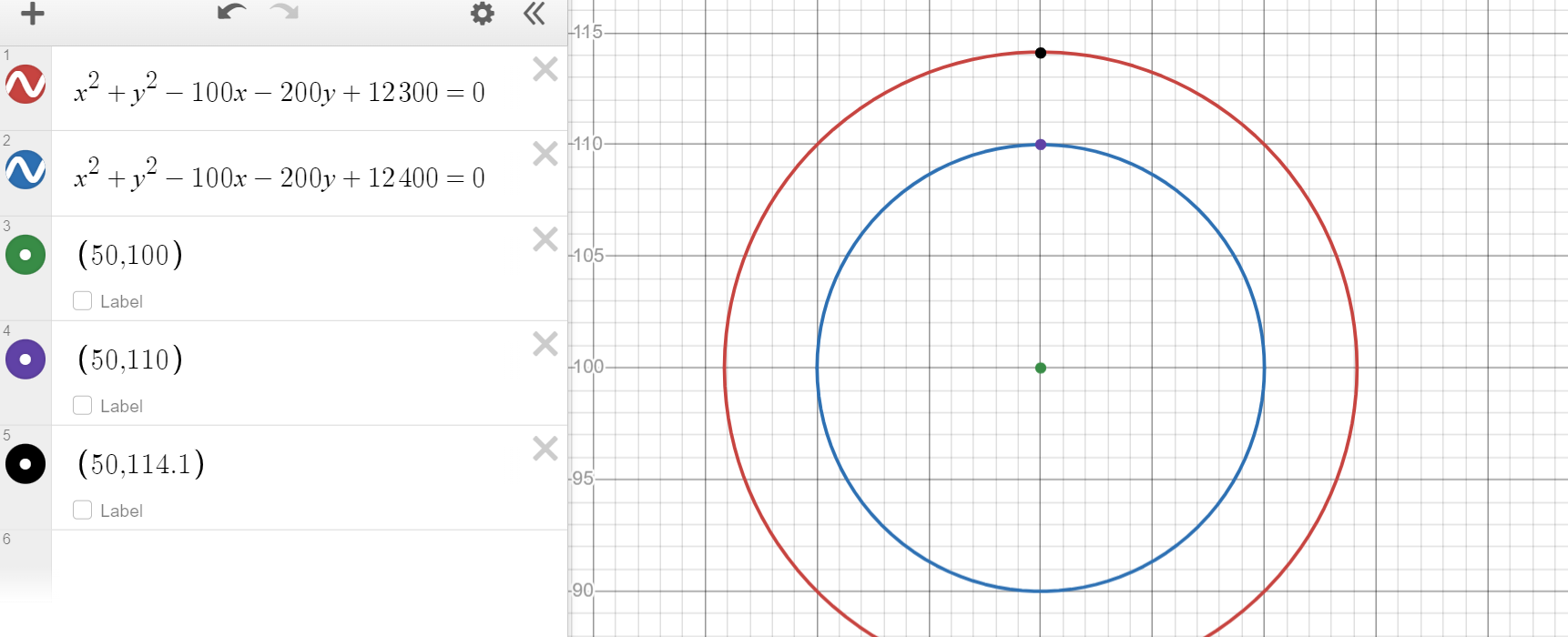
could be one approach but idts this is universally true
It is for concentric circles.
Line joining center and point on outer circle is diameter for the smallest circle (as it subtends right angle)
oh haan makes sense, nice approach
Oh yes, got it! Since the tangents are perpendicular to the radii, the circumcenter lies on the line joining P and the common center. Given the circles are concentric...the locus forms another circle, and the radius being half thus 5√2
+solved @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@1033329578564927529> (1033329578564927529)
Time
<t:1726666651:R>
Solved by
<@1075951732460376214> (1075951732460376214)
