30 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.However If roots are of opposite signs then product<0
a/4<0
a<0
So (-inf,0) is a possibile solution?
Initially I just did f(0)<0 giving a<1/3 but i realised the product of roots part just now
d is the correct ans
Let 2^x= t,
If x<0, 0<t<1
If x>0, t>1
Then we'll rewrite the entire eq in t, where t is positive and one less and other greater than 1
Condition lagane ke baad you'll get the ans!
Values of a manga hai not x
@itsav23
@SirLancelotDuLac
,rotate
Couldn't find an attached image in the last 10 messages.


,rotate
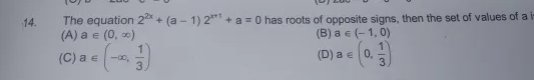
Assume $2^{x}$ is t, then you get $t^{2}+(a-1)t+a$ has one root >1 nd other in (0,1).
SirLancelotDuLac
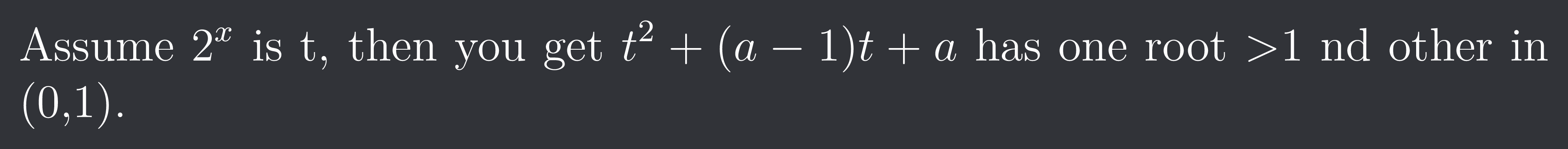
hows other in 0,1
both are of opposite sign
Note that x is of opposite sign, so 2^x we be >1 when x>0 and <1, when x<0.
oh u were talking bout t
Ye
Then you get:
1. Roots are real so, $a^{2}+1-3a>0$
2.a>0 and -(a-1)/2>0 as roots are greater than zero.
3.1+2(a-1)+a<0 as 1 lies between the roots of quadratic
first ones from discriminant
how did u get the other
2.Both roots must be greater than 0
3.1 lies in between both roots.
a>0 because both roots are positive so product positive too
Oh sorry I made a mistake. It is $t^{2}-2(a-1)t+a$
SirLancelotDuLac

sum of roots >0 too so -(a-1)>0
where did the 2 come from
ok so a>0 and 2(a-1)>0
SirLancelotDuLac
Woh 2^(x+1) hai toh 2^x*2 ho jayega.
3rd is f(1)<0
yeah
will solve it in a jiff just a sec
we went wrong somewhere
d>0, f(1)<0,a>0,2(a-1)>0
Let's call the functions f(x) and g(t)
f(0) < 0 should do the work but idk why g(1)<0 is not getting the job done
Well, if you call the functions that, then f(0)=g(2^0)=g(1)
The answer comes out to be (D) $a \in (0,\frac{1}{3})$?
SirLancelotDuLac

yeah
got that too
so to summarize it all first replace 2^x with t , call the new function g(t) then just do D>=0 , g(1)<0 , -2(a-1)>0 and a>0
all of it gives (0,1/3) , verified on desmos and matches the module. big thanx @SirLancelotDuLac
+solved @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@741159941934415883> (741159941934415883)
Time
<t:1726377127:R>
Solved by
<@1075951732460376214> (1075951732460376214)
