Monotonicity (AOD)
is there any other way of doing this problem other than manually keeping values in f'(x) as x=0,1 to check if it's increasing or decreasing in that interval
I understand they're checking f'(x)=0 at some point alpha to know that there exists a local minima at that point, but how would I know if that is the only point of local minima? how can I be sure that the curve will not meet again at x-axis after intersecting x-axis?
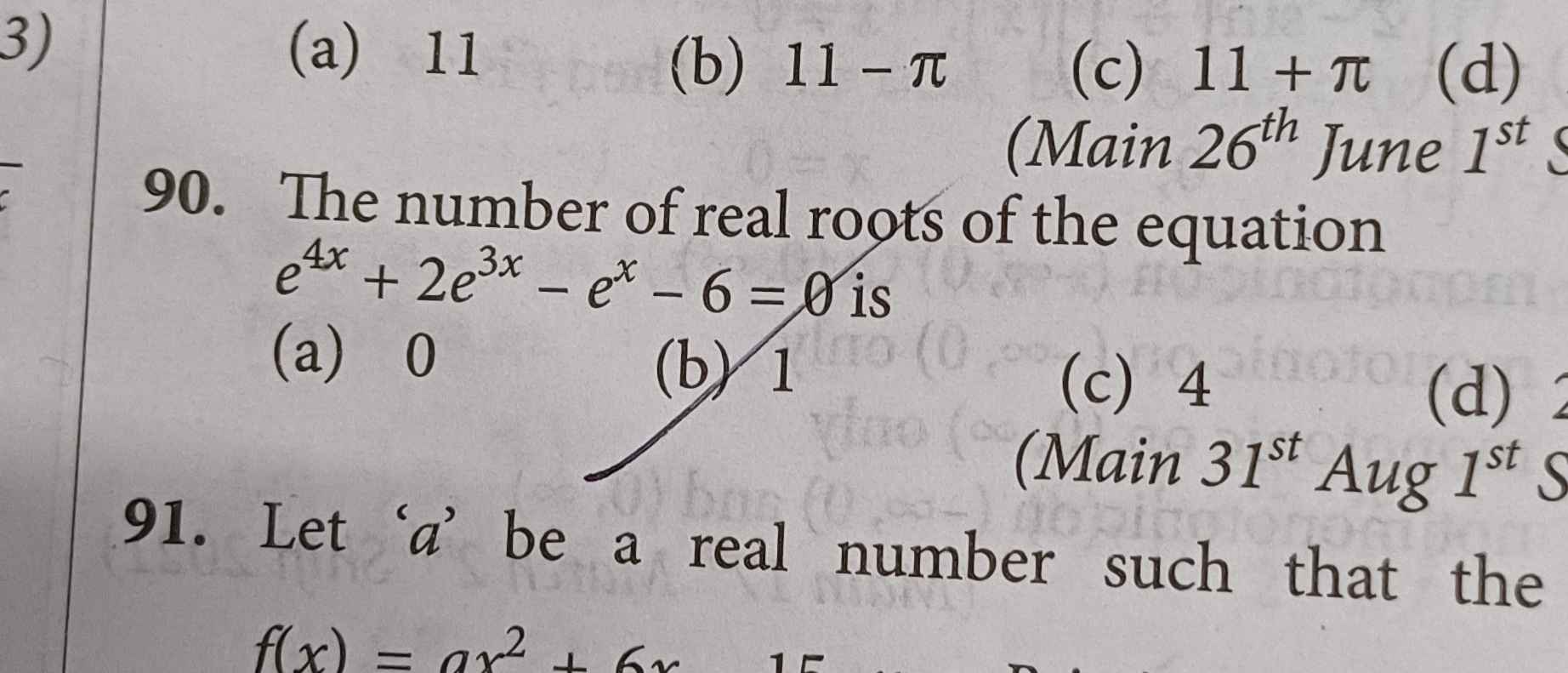
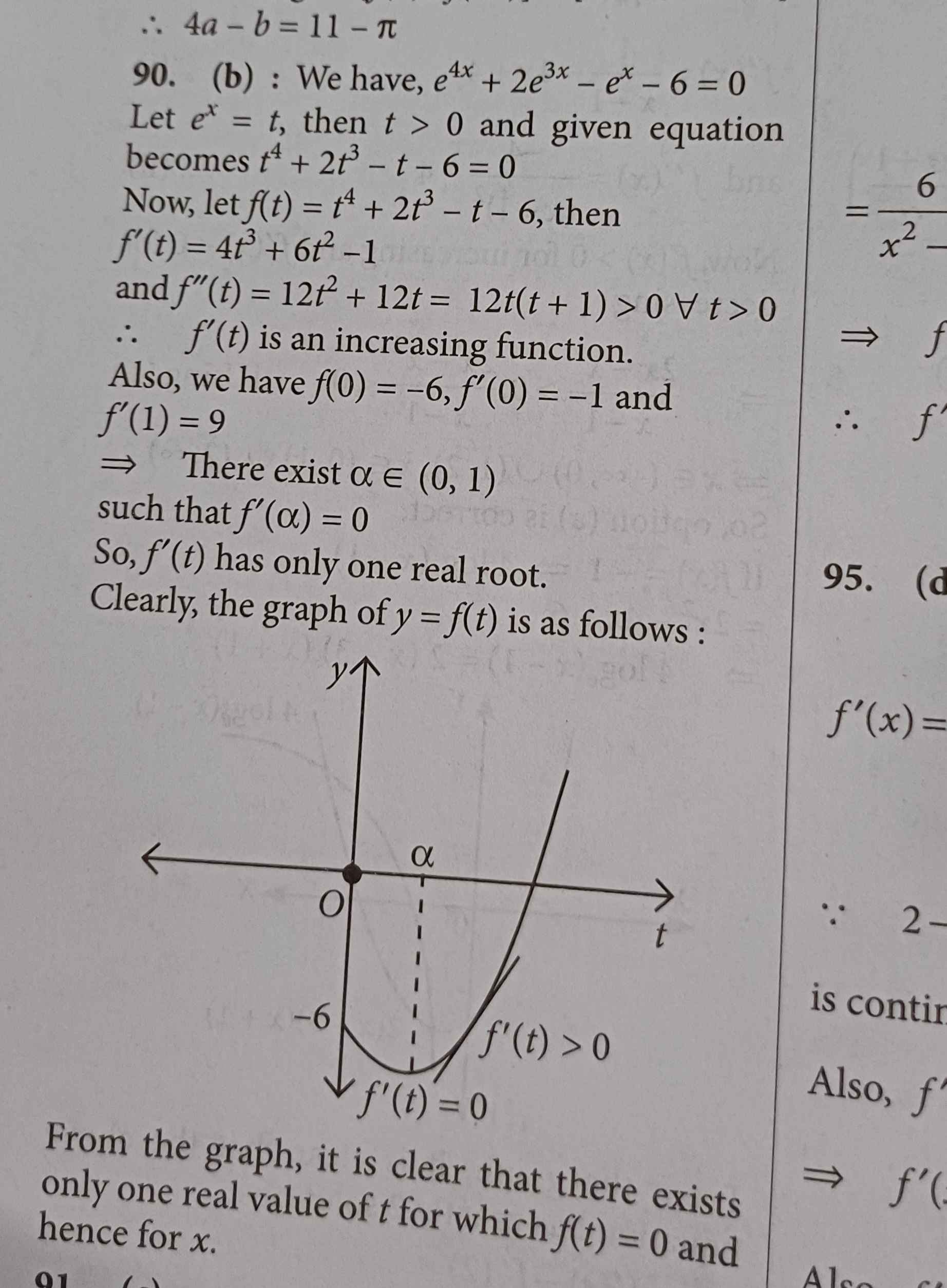
16 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.I hope there is at least one person capable of answering my doubt in this server 💀
Have you heard of Intermediate value theorem? @BlindSniper (BS)
yeah f(x) from [a,b] is f(a)+f(b)/2 something like that
but how is that relevant to this problem?
No this is not
If f(a)*f(b) < 1
Then f is zero for atleast one x between a and b
oh
but then from that you'll only know that it's increasing after local minima and it reaches x-axis
my doubt is how would you know if it's not going to touch the x-axis again?
Ok bro
*0
Wait isn't it something like if f(a).f(b)<0 then function is zero at least one point?
Or do I need to revise calc? :sweaty:
Oh yeah right
yeah exactly my bad i wrote f’
Am I like dumb to think we can solve by a lengthiet method of taking e^x as t and solve
but that's what we did?
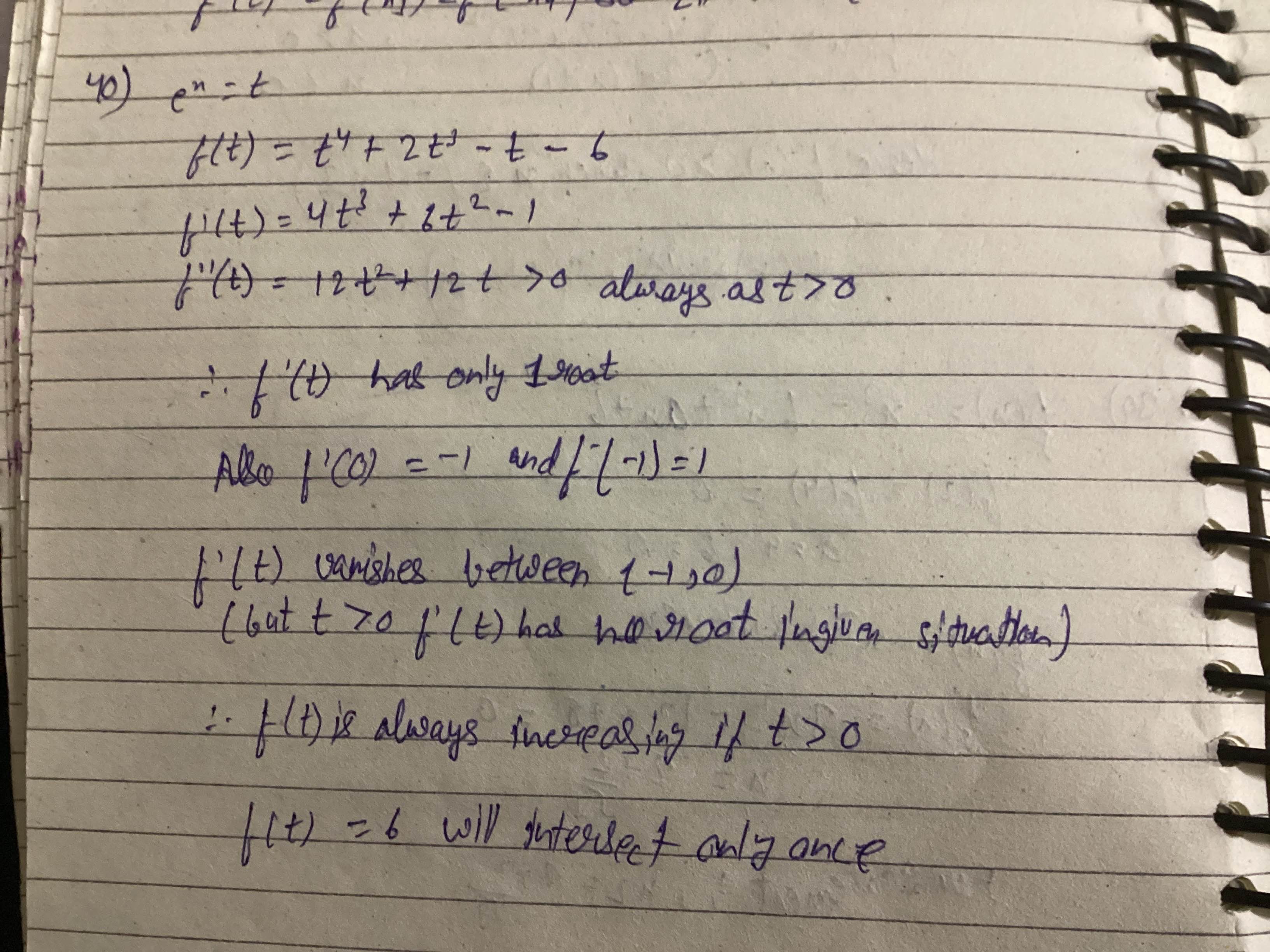
Isse idea lelo thodha
Mera solve krha hua h
oh wait
if f'(t) only has 1 root then it's only changing direction once
therefore it only passes through x-axis once
bruh am I retarded how did I not think of that
thanks anyway
+solved @Aman
Post locked and archived successfully!
Archived by
<@418393953742618631> (418393953742618631)
Time
<t:1726496194:R>
Solved by
<@1148479088521125939> (1148479088521125939)