circles
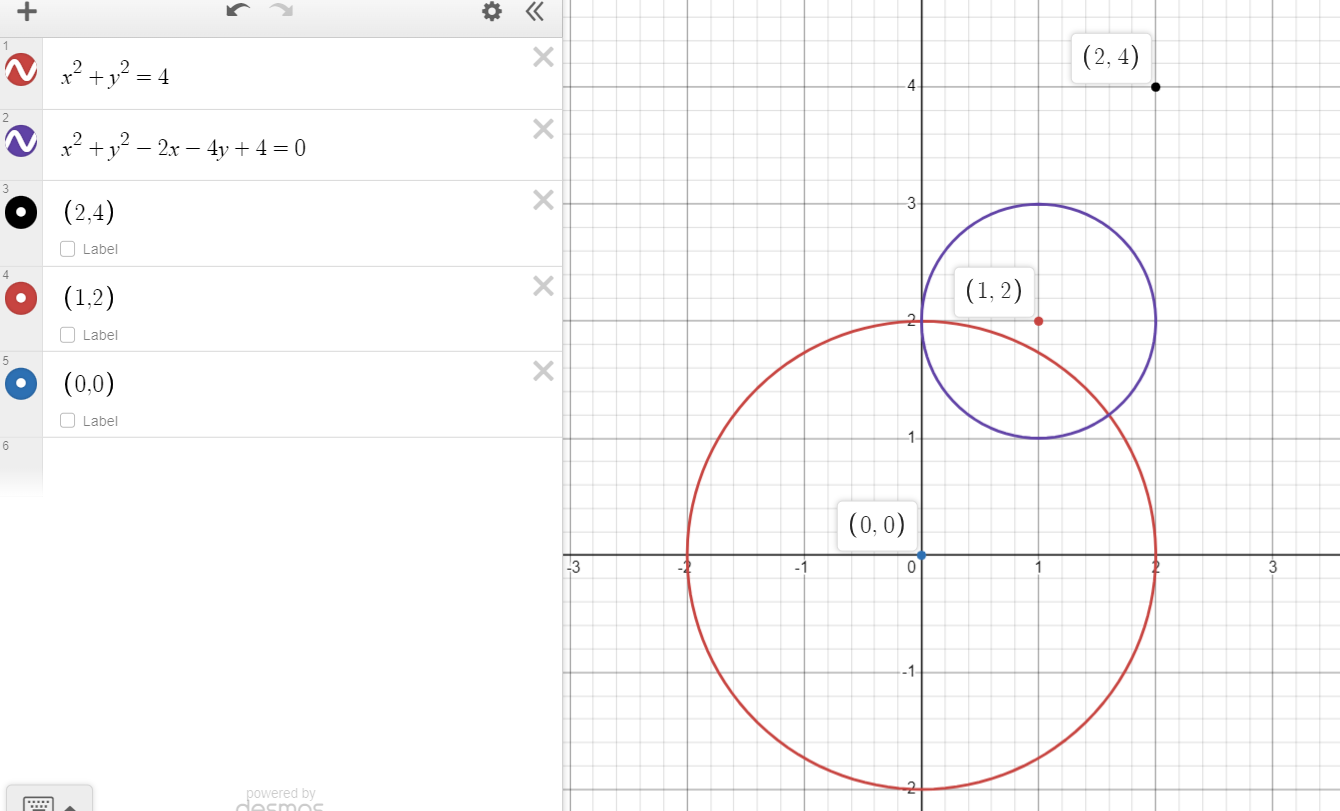
find the angle between common tangents of x^{2}+y^{2}=4 and x^{2}+y^{2}-2x-4y+4=0
i was able to identify centers and radii and point p which divided c1p:c2p in the ratio r1:r2 externally
after that i tried to determine slopes of tangents using point slope form for tangent but it gives only m=3/4
6 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.When we solve the slope equation
If we get 2 values, we're good
But if we get 1 value, that means the second value is undefined 🤯 and you can see in the graph, one of the tangent's slope is not defined (x=2)
Ans : So the angle between the tangents would be 90- arctan 3/4 <- Click This
write eqn of tangent in slope for for one of the circles, substitute x or y in the other circle's equation, D=0 as the line is a tangent to the other circle too, find the value of m, 2 values aani chahiye now tan theta= m1-m2/ (1+m1m2)
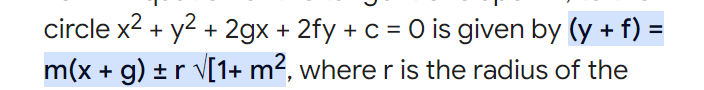
So 53 deg
Aight
Yep, 2 values of m werent were coming the above guy solved it tho
+solved @lim me → ∞
Post locked and archived successfully!
Archived by
<@741159941934415883> (741159941934415883)
Time
<t:1724155471:R>
Solved by
<@722854351600615465> (722854351600615465)