9 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.(c) 0?
f'(0)=$\lim{x \to 0} \frac{e^{\frac{-1}{x^{2}}}sin(1/x)}{x}=\lim{h \to \infty} \frac{(1/e)^{h^{2}}sin(h)}{1/h}=h(1/e)^{h^{2}}sin(h)$ Now solve this limit to get the answer
SirLancelotDuLac
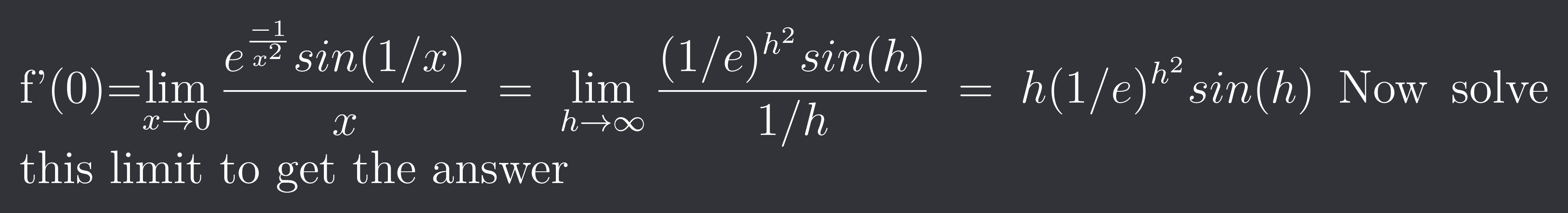
(Hint: Use the fact that exponential function of x increases very fast as compared to polynomial function of x)
1/e power infinity will become zero fast as compared to h in infinity in numerator so whole function will become zero
Right?
Yep.
So f'(0)=0
Okok
+solved @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@1165903904505081866> (1165903904505081866)
Time
<t:1722669958:R>
Solved by
<@1075951732460376214> (1075951732460376214)
