56 Replies
@πrate
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Hmm...
Seems to me multiply numerator and denominator by $sin(\frac{\pi}{2n})$ and then use $cos^{2}(A)-cos^{2}(B)$ to telescope.
SirLancelotDuLac

Why π/2n? I did try partial fractions with the denominator, but the numerator constants were just short of insane. And the sum didn't telescope properly, just partially.
It would be easier to use $cos^{2}A-cos^{2}B=sin(A+B)sin(B-A)$
SirLancelotDuLac
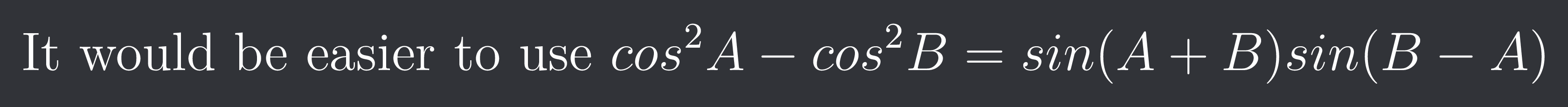
Oh, I misread.
That way if you take A=$\frac{\pi*K}{2n}$ and B=$\frac{\pi(K-1)}{2n}$
SirLancelotDuLac
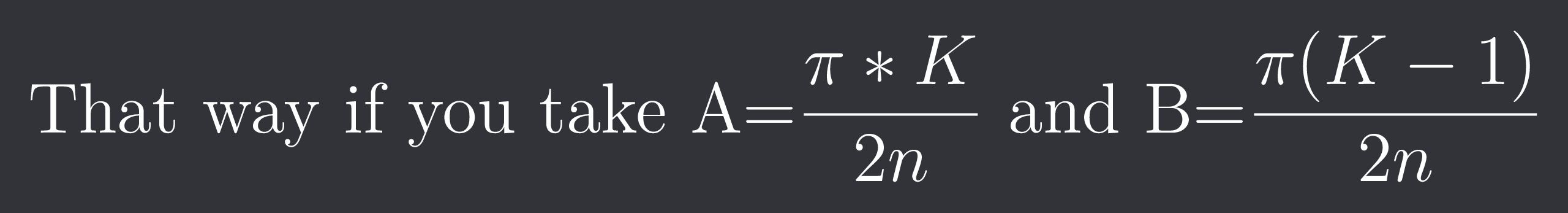
Wait, expand just the numerator? Wouldn't a telescoping series require the denominator to also be split?
When you do that you get something like $-\frac{1}{cos^{2}(\frac{\pi*k)}{2n}}+\frac{1}{cos^{2}(\frac{\pi(k-1))}{2n}}$
SirLancelotDuLac

This telescropes nicely.
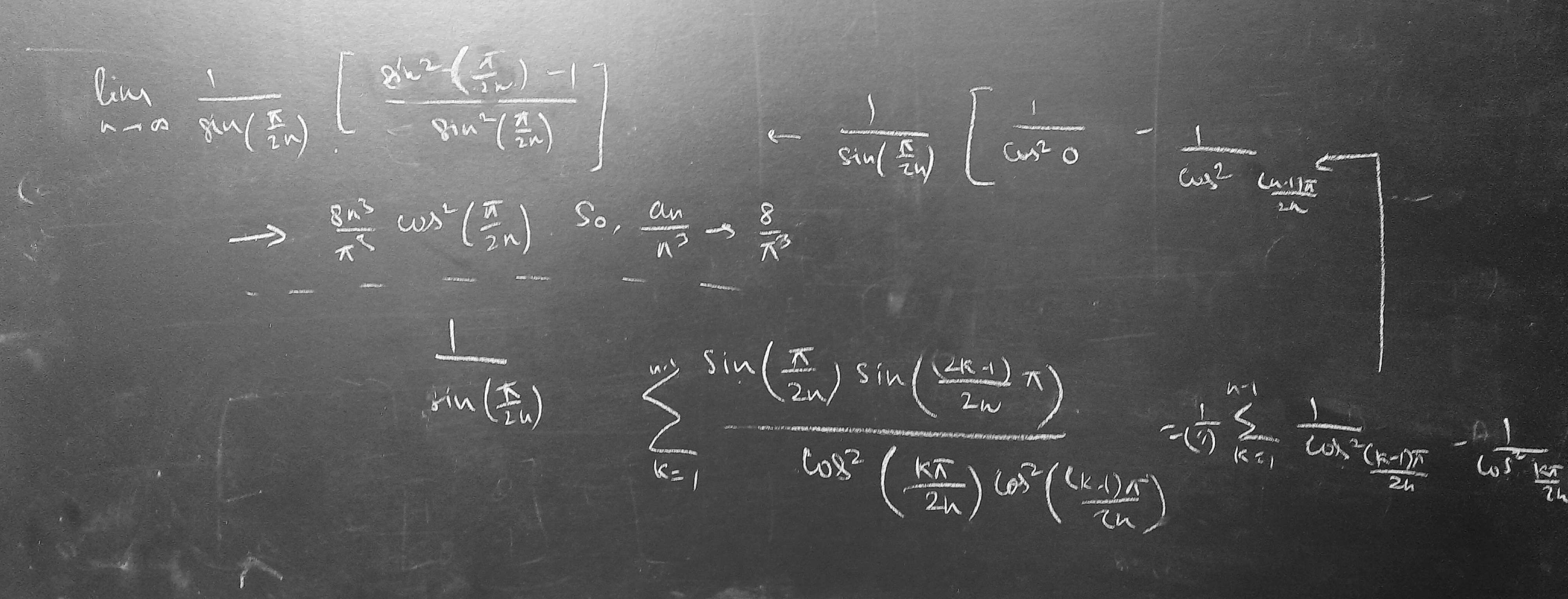
(Ignore calculation errors if any, but you get the idea)
nice
@Opt is it cleared?
Havent tried. Gimme a couple mins.
@πrate @SirLancelotDuLac I went through my fifteen or so pages of repeated working out to get the telescoping series. I figured out what mistake I made.
awesome
I am ashamed to say that I was trying to solve the question with the summand copied down wrong
i was not familiar with the term telescopic series till this question lol
You weren't? How?
hahaha
issok bud don’t beat yourself over it
didn’t know it was called that that’s all
like the term telescopic series
i just used to say write Tr as a difference of two terms xD
Oh. Yeah, I have to admit I haven't seen the term used a lot in Indian texts.
Well, I had a few other summations as well. (These are the bane of my existence)
feel free to share
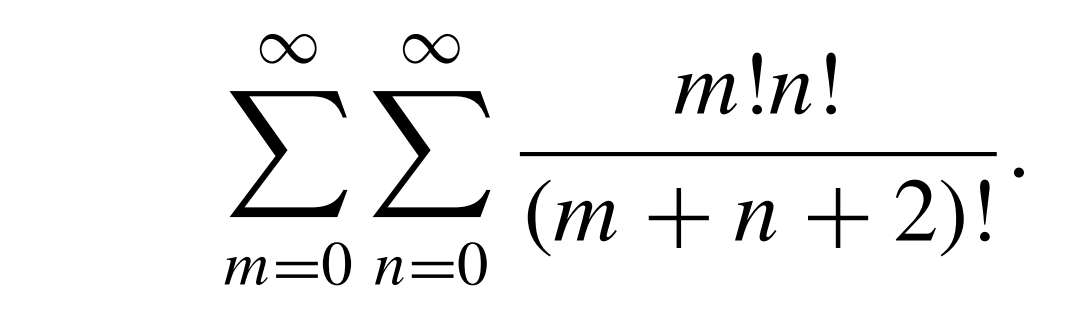
Once again, it's a clear example of telescoping series, but obtaining it in that form is extremely difficult imo.
@πrate
Im getting a really wierd answer to this one. 💀 But the basic premise is in the first summation, treating m as a constant, simplify to $\frac{m!}{(n+1)(n+2)...(m+n+2)}$, then write it as $\frac{m!}{(m+1)[(n+1)(n+3)..(n+m+1)]}-\frac{m!}{(m+1)[(n+2)(n+3)..(n+m+2)]}$. Telescope this and then it becomes easier
SirLancelotDuLac
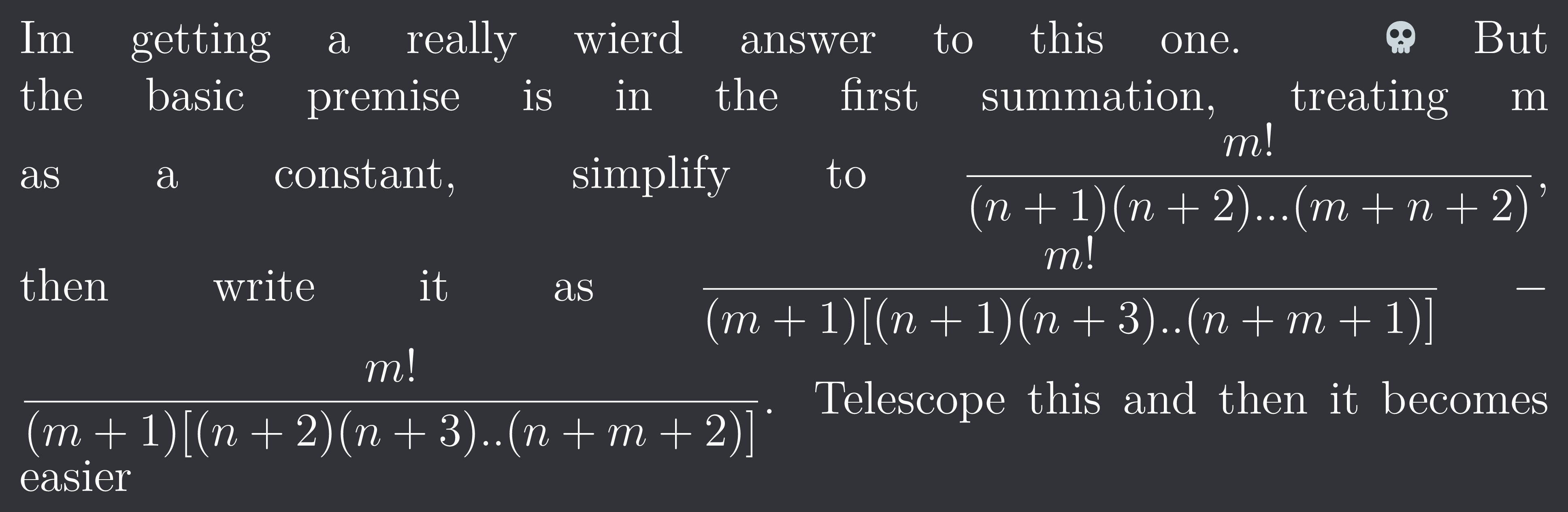
Oh that might help. We can then take the purely m terms outside the first summation
The problem is that it simplifies to $\sum \frac{1}{n^{2}}$, which is the basel sum but I don't think would be required for jee questions.
Oh this isn't a JEE question
SirLancelotDuLac
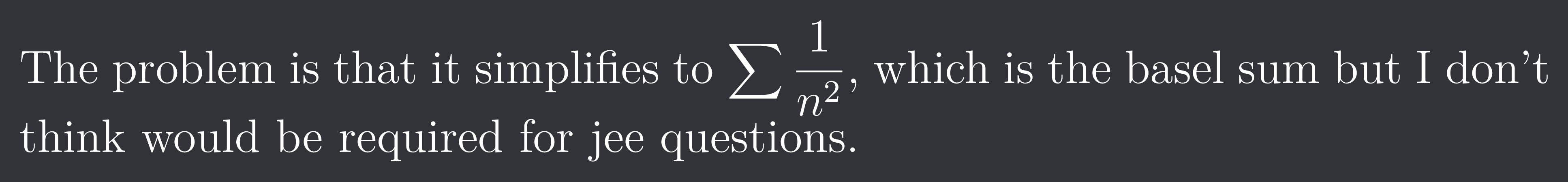
The answer is indeed π²/6
Oh. Then the answer might be pi^2/6
Thank you so much. But my question remains, how do you figure out the difference?
As in, product to difference conversion?,
.
No, in general
Well, many ways, but in this case, it was simplifying to 1/product of consecutive linear terms
So take the first and the last terms difference and multiply and divide by it in fraction
gives nice telescoping series.
So in short, just through observation?
Yes. If the terms were related somewhat via relation such as f(x+1)=g(x)f(x)+p(x), one would have taken a different route, dividing by g(x)^(x+1) and telescoping.
Btw, the trigo series was a Putnam question. 2019 to be precise. Found out just now.
I see. So just solving more questions of the type will help in any way.
Putnam questions are really fun to solve ngl.
True dat.
There was one from probability which i thoroughly enjoyed.
But, since we were doing summations, any tips for this one?
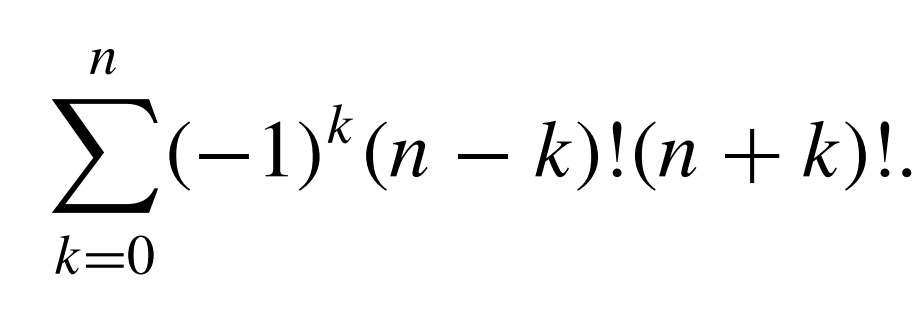
No fractions here
Pretty sure the answer needs to be a function of n.
Yeah. My bad...
sorry man had some classes ! just got free and pretty tired now ):
but i think @SirLancelotDuLac solved it
Hmm...We have to write here this as a sum of two things, and then things will cancel out.
Yeah, but doing that is one heck of a task.
@πrate sir, any tips for this? ('Cause I've tried this for a while and it seems non-intuitive)
nicely done @SirLancelotDuLac and pirate sahab
opt we good?
yo bro sorry for ping where do u get these qs tho?
Marking this as solved, if you want it to be opened batana
+solved @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@1035556259417571408> (1035556259417571408)
Time
<t:1722999767:R>
Solved by
<@1075951732460376214> (1075951732460376214)
