Proof of Irrationality of π
What is a simple approach to prove the irrationality of pi? Can one also provide an insight for basic idea about how to go about proof of transcendental irrationality?
9 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.I remember seeing a wiki page on this funnily enough but none of the proofs are as simple as one would want. They are pretty simple, but not elementary
https://en.m.wikipedia.org/wiki/Proof_that_%CF%80_is_irrational
I saw that too but yeah, they are very non-intuitive.
I tried using continued fractions and doing smth but to no avail.
Hmm...
It is infuriating I have to admit
I think Niven's proof is quite elementary.
(For my future reference:) Proof goes about assuming π=$\frac{a}{b}$, a and b $\in$ Z, we assume a function:
$f(x)=\frac{x^{n}(a-bx)^{n}}{n!}$, we define another function g(x)=$f(x)-f'(x)+f''(x)+....=\sum{(-1)^(k+1)f^{k-1}(x)}$
We show properties 1 and 2 on g(x):-
1. g(x) is always an integer at x=0 and π
2. $\int{0}^{π}f(x)sin(x)dx$=F(0)+F(π)
Now set range on $\int{0}^{π}f(x)sin(x)dx$ and show that for sufficiently large n, the values lies between 0 and 1, hence it can't be an integer. This is contradiction to result 2. Hence proved
SirLancelotDuLac
Compile Error! Click the :errors: reaction for more information.
(You may edit your message to recompile.)
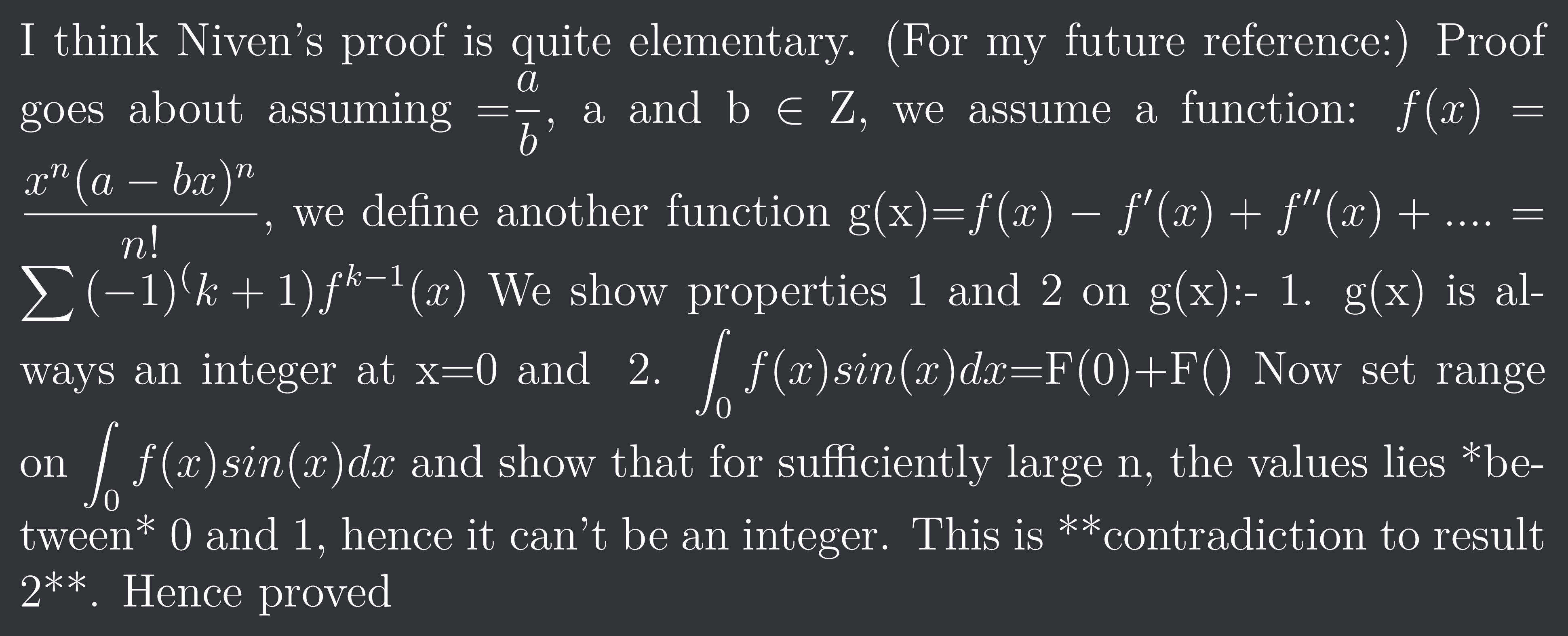
+solved @Opt
Post locked and archived successfully!
Archived by
<@1075951732460376214> (1075951732460376214)
Time
<t:1719235957:R>
Solved by
<@763645886500175892> (763645886500175892)