32 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Sigma n
Excuse me what? No it is not n(n+1)/2
Umm I think doing it in my mind it is
It is not.
n(n-1)/2
...no it is not.
No. You have to see the values n(n+1)/2 aquires. It is basically something like this: if you have to find the kth term, find n such that n(n+1)/2=k. If n is an integer, you are done and the value of kth term is n itself, otherwise, you have to do floor(n)+1
It is the basic premise of the question
$n^{2}+n-2a=0$. So, n is $\frac{-1+\sqrt{1+8a}}{2}$. Therfore, the ath term would be $[\frac{-1+\sqrt{1+8a}}{2}]+1$ if the expression is not an integer and $\frac{-1+\sqrt{1+8a}}{2}$ if it is an integer.
SirLancelotDuLac
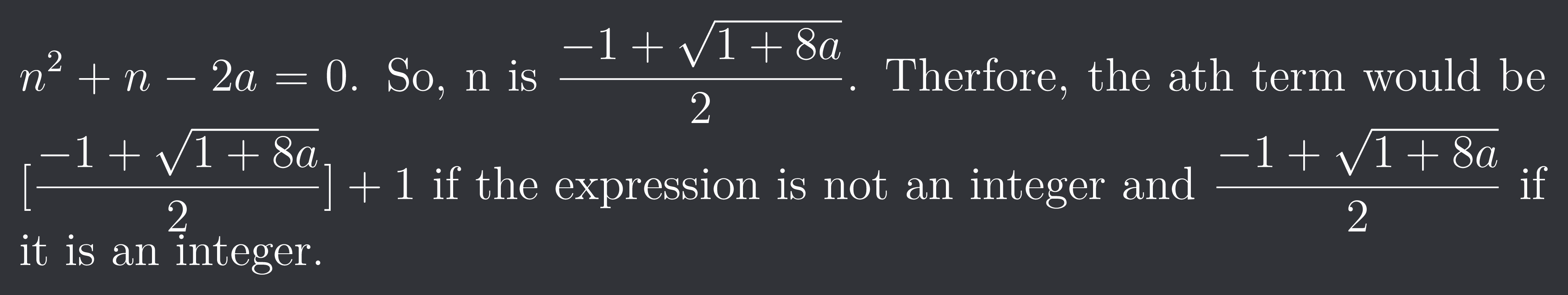
Or ceiling of $\frac{-1+\sqrt{1+8a}}{2}$
SirLancelotDuLac
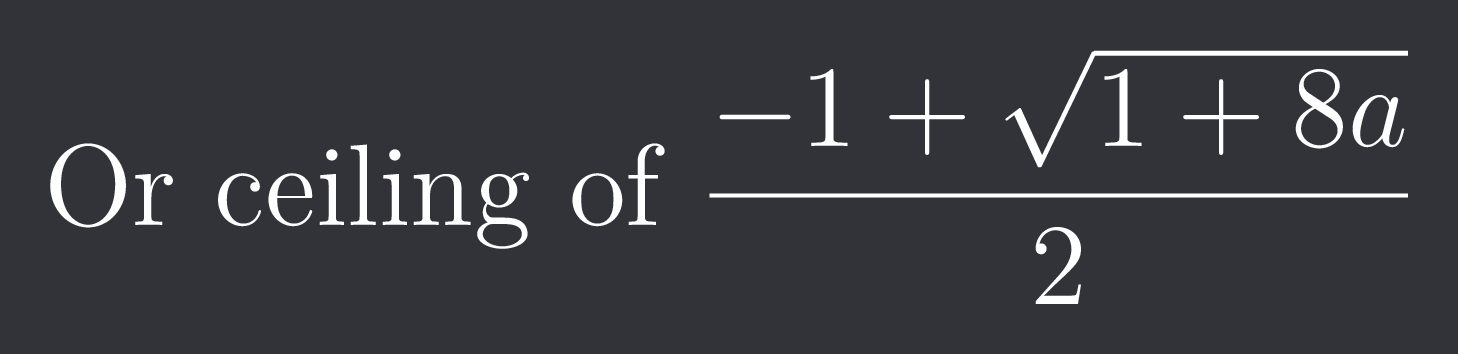
Wait, why is there a +1?
Where? Can you please specify?
If you mean where the value of n is not an integer, you can think of this like this, n=5.5 implies 5 natural numbers have already come before n and n is somewhere ahead of the last 5.
No, i understood the floor. But why +1?
Floor (aka integral value of n) tells you how many natural numbers are behind n. You have to add +1 to the number of naturals behind n to get the value of n
Oh that's what I missed.
I got everything until floor((1/2)(√(1+8r) -1)) but then I didn't add the 1
I'm very sorry, but can i ask the source of the question?
Putnam and Beyond.
Oh. Thanks.
One more question I'm struggling with in case you'd like to try.

148.
Can we use calc in this?
You can use whatever you want
Well, the function is 'anti-symmetric' about x at a distance of $\frac{1}{n}$ for all x
So, I guess that would help
SirLancelotDuLac

@Opt This doubt is resolved right?
In this one, we claim that a line intersect non-linear polynomial graph at only finite number of points, but all points for form $(x-\frac{k}{n},P(x-\frac{k}{n}))$ form on a line (as $P(x-\frac{1}{n})$,P(x) and $P(x+\frac{1}{n})$ are in A.P), so this line intersects graph at infinite points. So graph must be linear and hence polynomial is P(x)=cx+b
SirLancelotDuLac
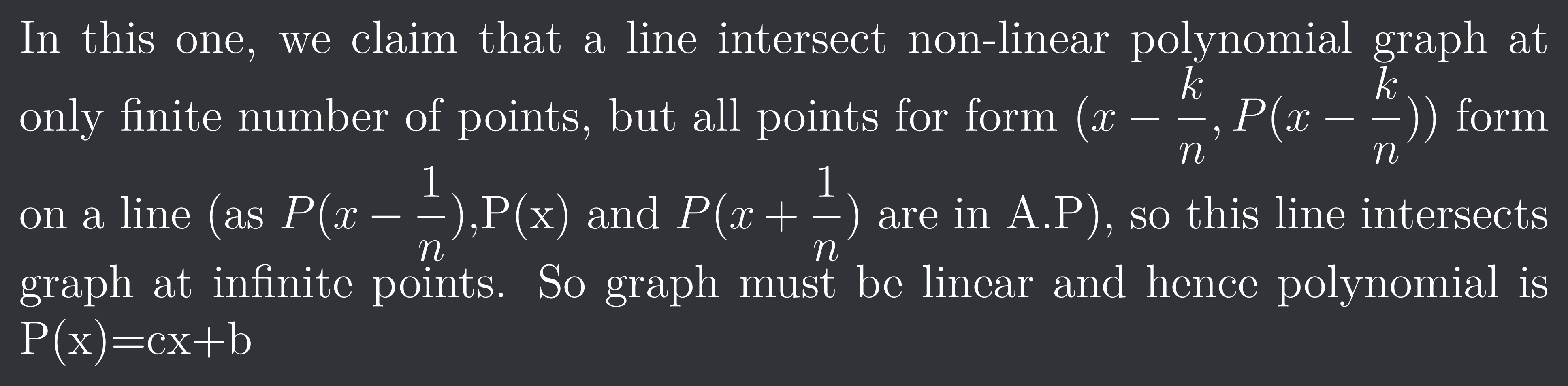
Not necessarily. n is an integer so we can have, say, a wave, that intersect all points 1/n along the line, but not the others.
It is given P(x) is a polynomial. You cant have a wave extending infinitely in a polynomial.
Further, one can also imagine the graph being monotonous after a certain point. In this region, for a non linear polynomial, graph increases non-linearly (Hope that makes sense.), so the graph will not be able to cut that line again after an intersection. This is not our case as stated above.
Oh I see.
+solved @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@763645886500175892> (763645886500175892)
Time
<t:1719230937:R>
Solved by
<@1075951732460376214> (1075951732460376214)
