limits
/tex
\definecolor{a}{rgb}{0.24313725490196078,0.7725490196078431,0.8}
\definecolor{b}{rgb}{0.0,0.46,0.5}
\setlength{\fboxrule}{0pt}
\pagecolor{b}
\color{a}
find n such \ that \lim_{x\to 0}\frac{\cos^2{x}-\cos{x}-e^x\cdot\cos{x} + e^x - \frac{x^3}{2}}{x^n} \ \ is finite
find n such \ that \lim_{x\to 0}\frac{\cos^2{x}-\cos{x}-e^x\cdot\cos{x} + e^x - \frac{x^3}{2}}{x^n} \ \ is finite
12 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Ansh Agarwal
Compile Error! Click the :errors: reaction for more information.
(You may edit your message to recompile.)
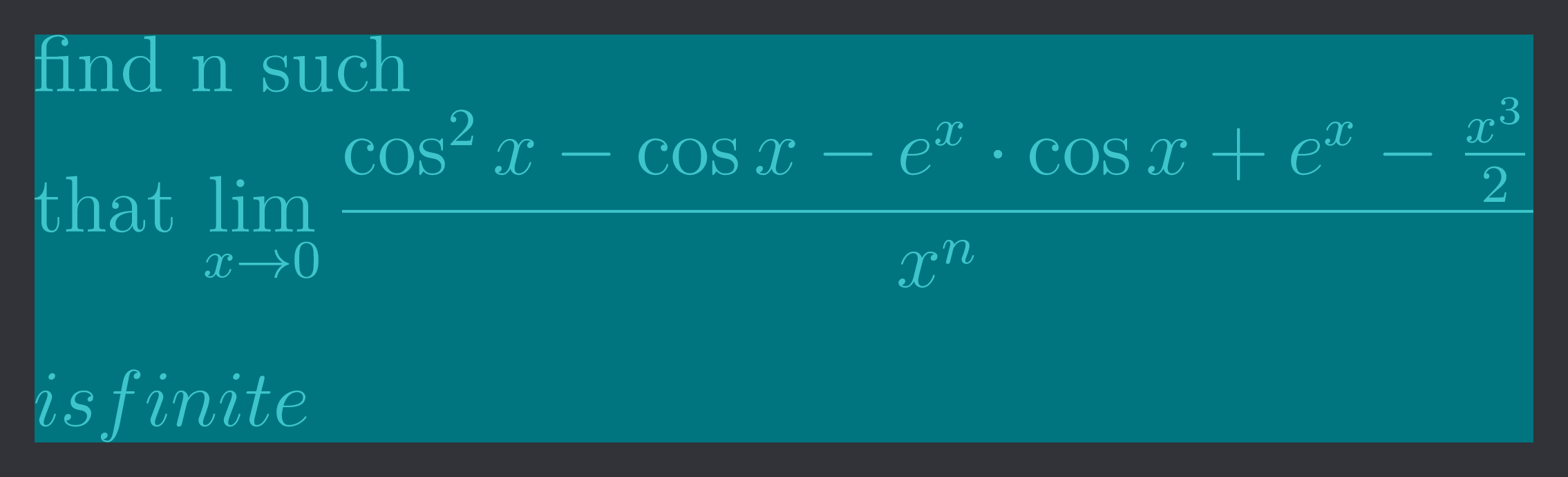
It shall be maximum positive value of n imo
The answer is 4
n is a natural number is given
@Ansh Agarwal did you try taylor series
To no avail, didn't give the answer.
Taylor would work i guess? Numerator tends to
$(1-\frac{x^{2}}{2})^{2}-(1-\frac{x^{2}}{2})(1+x+\frac{x^{2}}{2})+(1+x+\frac{x^{2}}{2})-\frac{x^{3}}{2}-(1-\frac{x^{2}}{2})$
SirLancelotDuLac
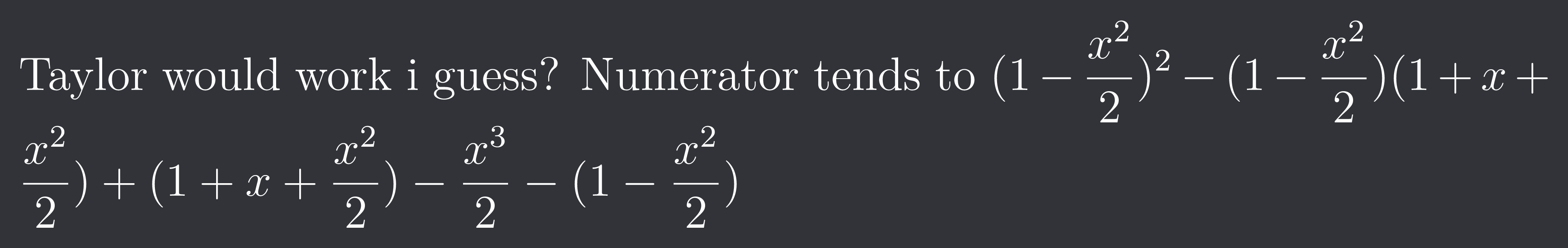
This comes out to be \frac{x^{4}}{2} so min. value of n is 4 and value of limit at that is 1/2.
Further L' Hopitals works out as well.
Thanks, it worked , probably made a mistake or something the first time
+solved @SirLancelotDuLac @Optimus43
Post locked and archived successfully!
Archived by
<@783738581578940437> (783738581578940437)
Time
<t:1719165530:R>
Solved by
<@1075951732460376214> (1075951732460376214), <@886554076521840650> (886554076521840650)