15 Replies
@Apu
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.This is indeterminate of the form $1^{\infty}$ so on numerator it tends to $e^{(\frac{5x+4x^{2}}{x})}-e^{(\frac{5x-4x^{2}}{x})}$=$\frac{e^{5-4x}(e^{8x}-1)}{x}$ which tends to $8e^{5}$ as x tends to zero.
SirLancelotDuLac
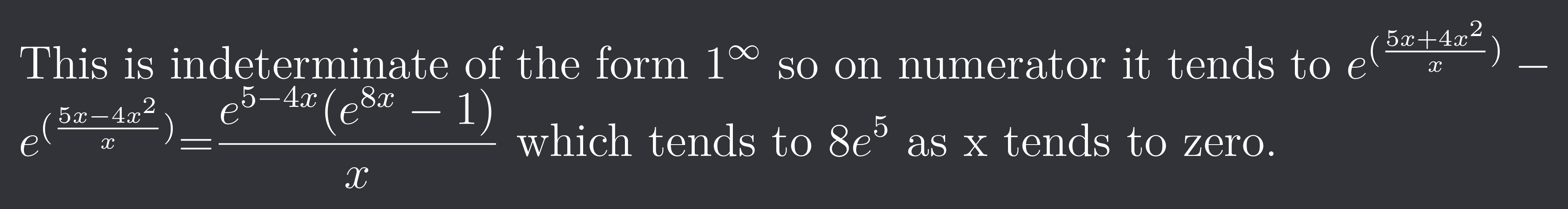
Bro where did lim x->0 gone
The two brackets in numerator are 1^infinity form and then I have shown the solving
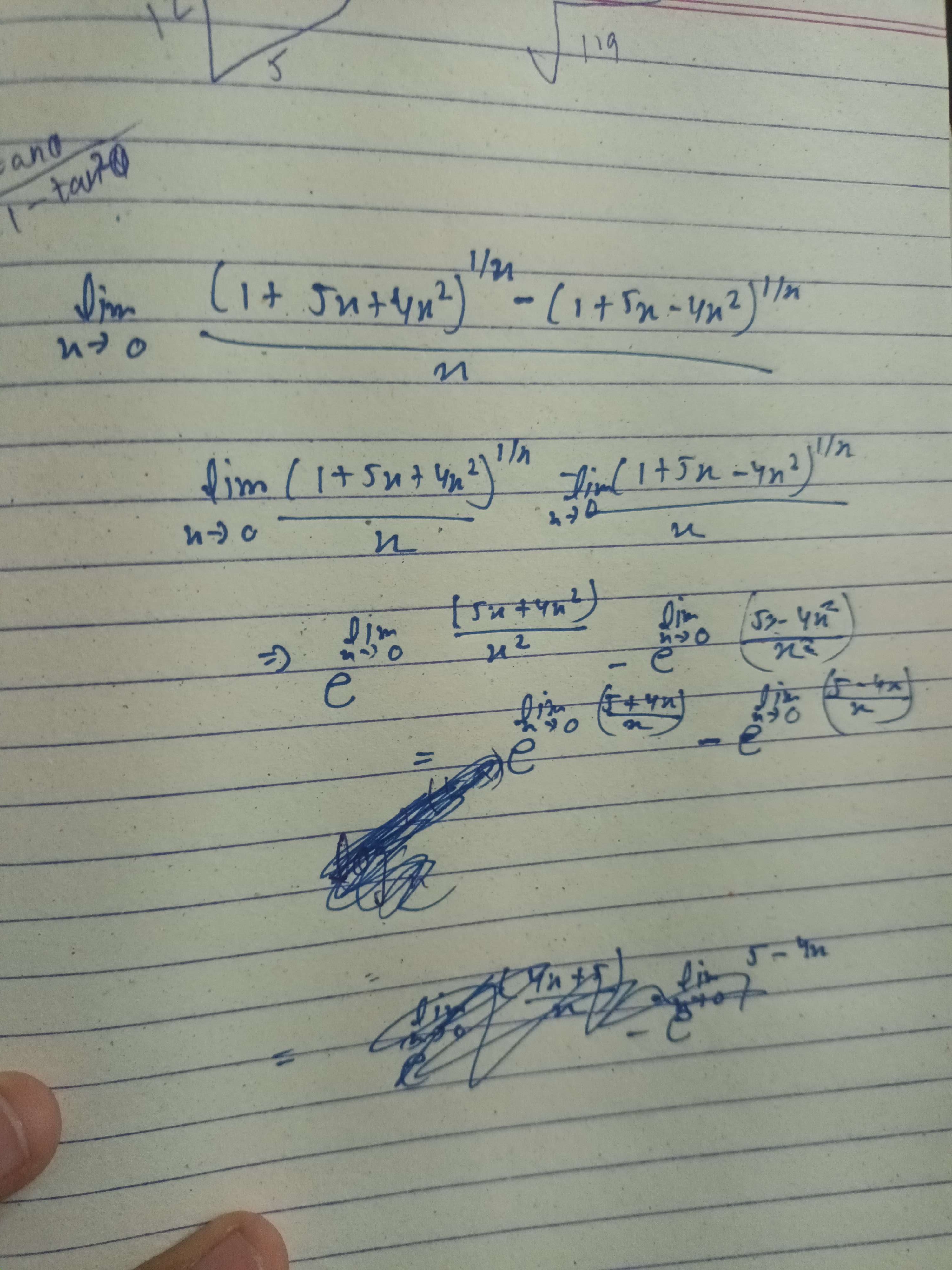
See I did this
Yes this is half the solution. Now the numerator tends to e^(5+4x)-e^(5-4x)
So you basically take out e^(5-4x) common to get answer
There's x also in denominator

Oh ok
i forgot that formula existed i was trying to diffrenciate the thing 💀
thanks
+solved @Aman @SirLancelotDuLac
Post locked and archived successfully!
Archived by
<@726641475080683522> (726641475080683522)
Time
<t:1718692156:R>
Solved by
<@1148479088521125939> (1148479088521125939), <@1075951732460376214> (1075951732460376214)
