81 Replies
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.this is a really good qn, i saw this case on a physics galaxy video... i dont remember its soln still but ill link the video for you if you wanna check it out
https://www.youtube.com/watch?v=gNoaUQaVDvM&list=PLYVDsiuOZP5p6fmdFyKhc2di1AMQZZEaU&index=26\
Thanks. Will give it a look.
Apologies. The video has the case of a ring with angular speed, not a sphere.
But sir gave: Effect Current = Q.(omega)/2pi
@KaiZên the one he discusses is the magnetic field inside the sphere
I managed to solve that. Rather easy integration. But what is troubling me is the magnetic field outside. It's non-negligible. So no, "Solenoid ke bahar magnetic field zero ho jaata hai" business here.
@Opt have they asked B field function at distance r along the rotational axis itself?
or radially?
It's asked as a function of the position vector r
yup so its radial.....
but also consider this:- here it is asked as a radial function....so its not that direct ☠️ .
I did, but it's the magnetic vector potential, not the field
vector potentiel? potentiels are scalar right?
No no, vector potential


And it's spherical coordinates
I think the person who sent me this question was high or they just randomly made it up
The magnetic vector potential is defined as the vector field the curl of which is the magnetic field.
oh wait u meant in that terms-
i did read that in griffiths 😄 ( i thought you meant standard potentiel term ☠️ )
This is from Griffiths lol
griffith op 🔥
The solution I just sent I mean. Not the question
True.
yeah. if you are looking for on axis B field its easy enough just integrate all the rings.....
Yeah it's a hell of an issue outside the shell.
good to see someone using griffith! give it a read (especially where they derive the amperes circuital law eqn from biot-savart law!) its entire rollercoaster of visualisation man...
especially radial i would say ☠️
Ye it is. I started with Feynman's Lectures, then moved onto Griffiths.
you are on right track man 🔥
Feynman's Lectures Vol.3 remains untouched lol
Spin samajh hi nahi aaraha. No matter how I try to understand
ill try to link a source.
One more thing. In this question, can we consider the magnetic moment and use the electric dipole comparison method?
i was thinking the same thing tbh....it should work considering a sphere of rings is just a distorted solenoid..
But the solenoid radius is varying.
This is just nightmare fuel you have to admit
yes thats why i said "distorted"
i do admit ☠️ (mathmetically)
the thing is the magnetic field is not uniform at every point at a dist r.
amperes law doesn't seem to be useful and neither is integration wala method useful ig.
as the field varies everywhere
let me try once k?
its asked as a function in r right?
I might have misunderstood the question I have to admit
I assumed position vector but it does just say r. Could be cylindrical coordinates for all I know.
Then it would be uniform due to symmetry.
i still think the question asks radial....
magnitude pucha hai that makes it so that the question wants you to find everything in terms of r and R
Since it was a sphere i assumed spherical coordinates
Yeah, but it also mentions angular velocity along Z so maybe they want in terms of distance from Z axis?
This question is probably bakwaas.
intresting i would call it 😄
uss case ke the problem becomes easier but still is very very difficult afaik
Let me try again.
@Opt are you aspiring for JEE 2025?
Yup
nice
@Opt it should work. maine magnetic moment wala part kar diya. substituting it would work imo, with theta as parameter......(only in one plane of the sphere).
Theta is polar angle or azimuthal?
in fact if you think rotational diameter ke about toh symmeteric he hai....
does that make the process easy?
It does. Symmetry is always appreciated
yes why not?
polar (the same that appears in E field due to general point due to electric dipole).
Angle between r and z right?
the reason i think it should strongly work is imagine like this, there has to be a solenoid of certain dimension which can exactly replicate the B field pattern due to this sphere....like if i put both of em into a black box, we wont be able to identify which is which.....
the dipole moment vector...yeah
have you ever tried this for a bar magnet? for a general point?
So how do we figure out the magnetic moment now? idA?
i have calculated should i send?
Not yet. Still doing Magnetic Effects of current.
Gimme a clue I'll try.
oh....a nice way of it is shown in ncert of the magnetic effects of earth chapter
consider a direction for area vector of the rings.........then chose polar coordinates thru centre, divide into rings....find the current in them using sigma......and add em all up (integrate directly they all would be pointing in same direction as the rings are directly stacked over each other..)
like to find the B field due to a bar magnet, what they did was they found the magnetic moment of it, then in the formula for E field due to electric dipole, they replaced e0 with u0, and p with m.....and viola you get the exact formula for B field due to bar magnet! amazing how symmeterical electrostatics is with magnetostatics 😄
Oh that. I've done it before. Its also nice to do it for a current carrying ring, to find field on the plane of the ring.
yup!
@Opt once you get the formulation of m vector for this sphere...do drop it here once!
I think I messed up because I got an odd function as the integrand.
you would get a cos^3 term imo
my function matches dimensionally as well....
I got a sin³θ term
Wait. Think I set the bounds wrong.
yeah same thing you would have taken the angle differently....
-pi/2 to pi/2 for the entire sphere....(in my system)
wait sorry in your angle terms it would be 0 to pi
Ye zero to pi.
I got this.
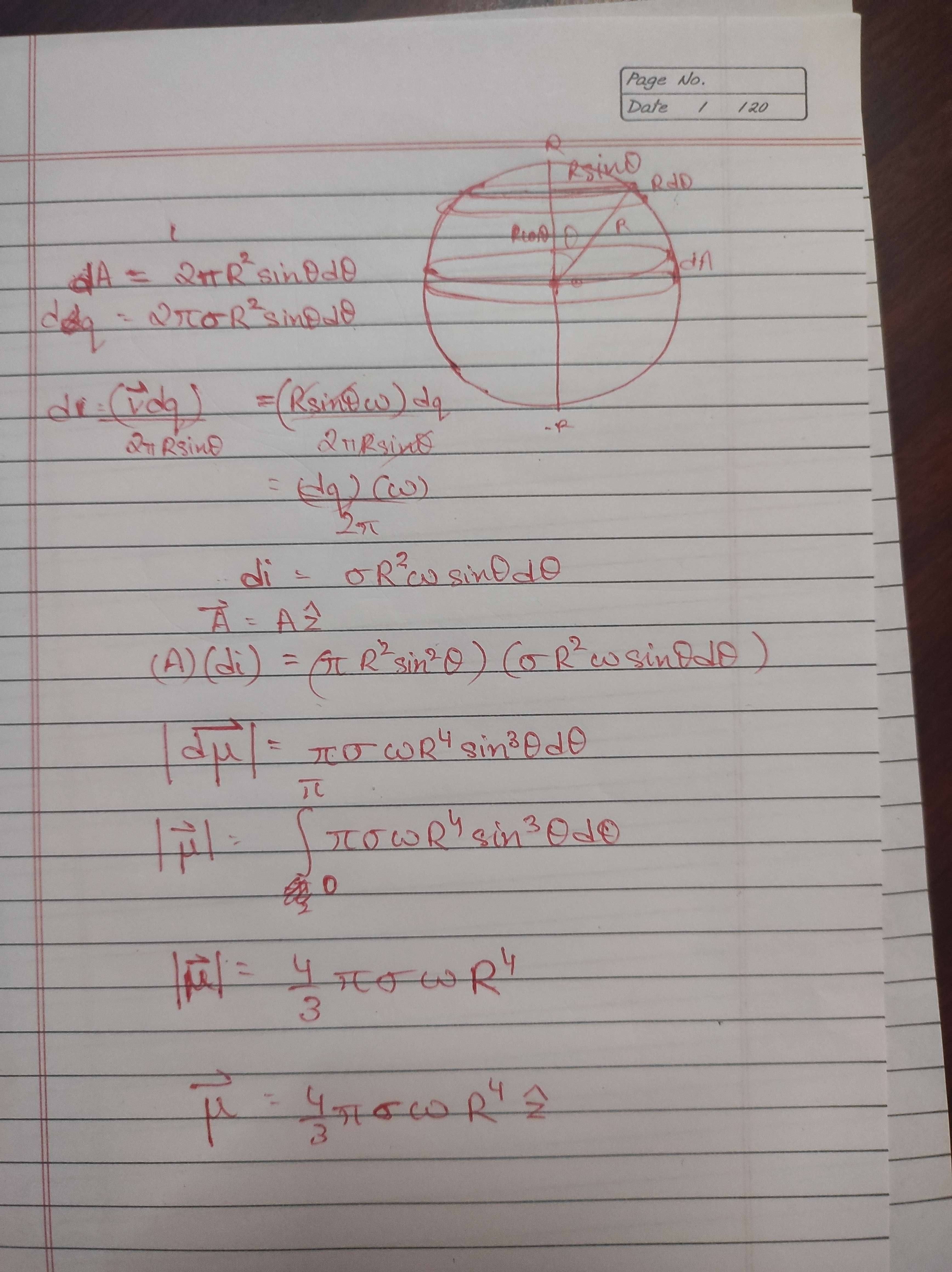
way to go bud its correct! same as the function i got.
Yeah I took -π/2 to π/2 originally which is why I got zero. Bounds error
now put it in the function of E field due to dipole at general angle theta, replacing p with m vector, and like e0 with u0....then we shall achieve i think the answer to this 🔥
no prob it happens with me also sometimes 😅
We'll be using the formula for the field along the equatorial plane right?
-pK/r³
yup (kp/r^3 root 1 + 3cos^2(theta)) one
Oh generalised. I never use that because I forget what the numbers are. I just resolute and write in vector form
yeah sure! even i dont encourage to learn it....would be better to add the two vectors to get the net sum
👍
if you want at equotorial only...then yes!
i hope your query is solved @Opt ? did you get the final vector expression? do send it once here when you derive it!
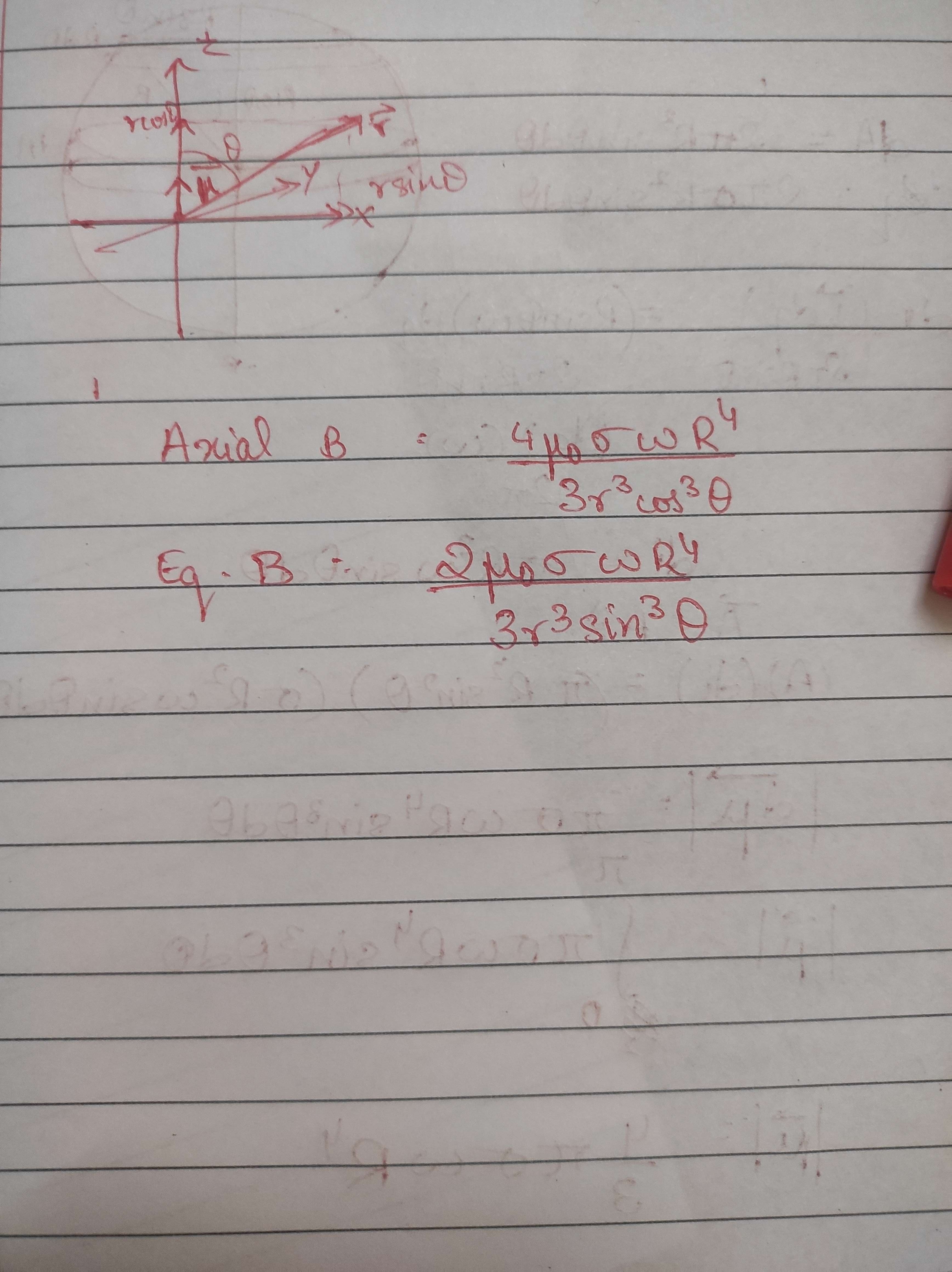
Just the magnitudes.
thats would be enough! the vector directions you can easily specifiy based on the tangets to field lines.
Yup. And because it's magnetic field, cross product rules come into play again. Pain in the neck.
No wait they don't. Because dipole moment.
always keep in mine calculating m whenever u see a straight up magnetic dipole (although, this is the case everywhere) like field structure, would be far more easier than calucaluting B field thru individual elements..... 👍
yup
Using a surface current element for this question would be hell incarnate
☠️
Derive k, construct kdA, biot-savart law, die about four times etc etc
yup.....thank god magnetic field generators always exist as dipoles to save us loads of work!
Thanks mate.
🙏
+solved @Deleted User
Post locked and archived successfully!
Archived by
<@763645886500175892> (763645886500175892)
Time
<t:1718596650:R>
Solved by
<@1221329740959318107> (1221329740959318107)
no worries! feel free to post other doubts as well 😄
