38 Replies
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Ye konsa image format hai?
Pta nhi
Convert to jpeg and share please
can you please send in some other format? it aint opening on my laptop....
Nope, still the same.
Bruh wait
ok 🙏

There you go. That should work
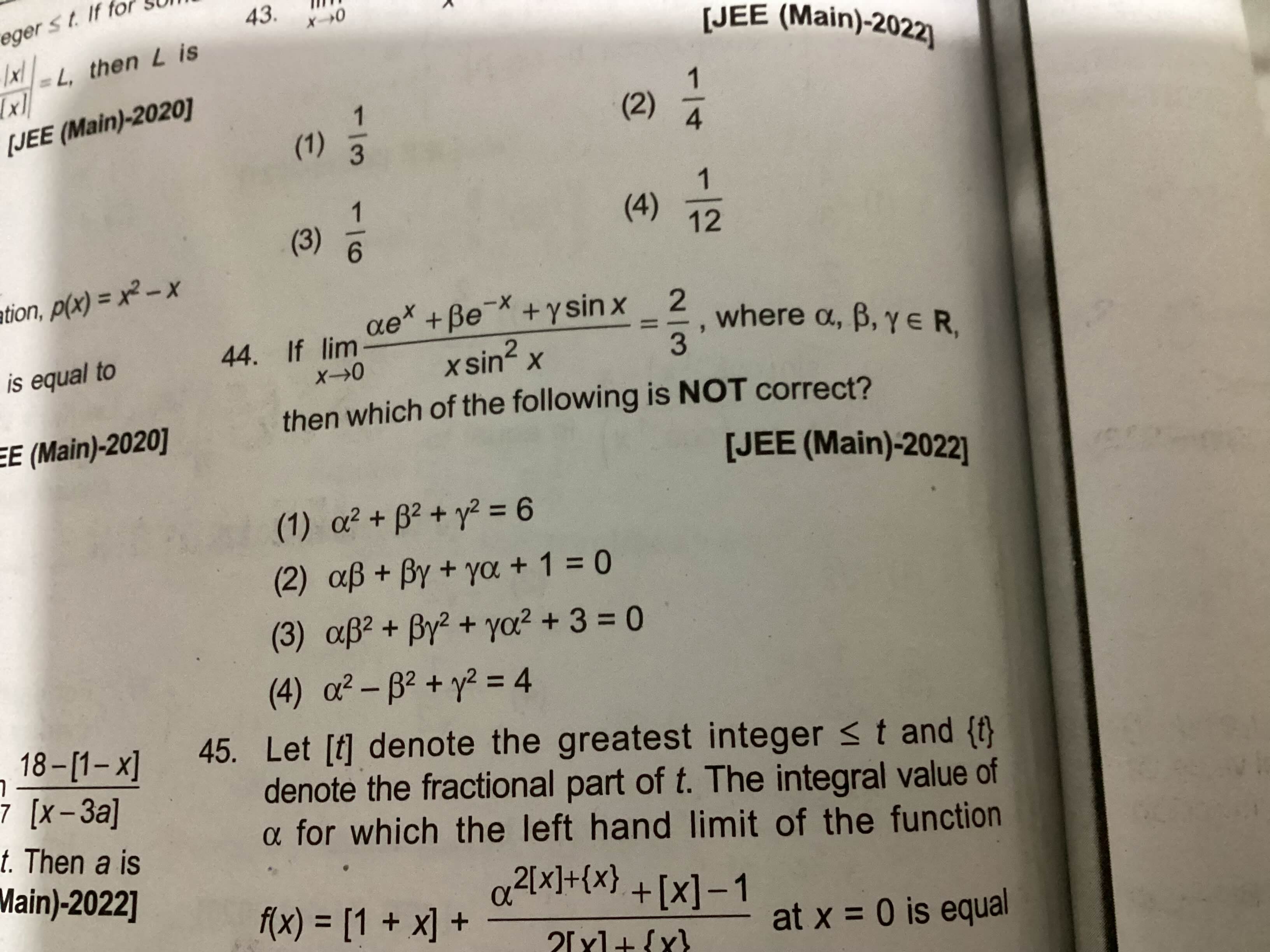
44
I got the equations
α+β=0
2α+γ=0
For now
Solving the limit currently.
Use expansion and make linear equations.
$\frac{(ae^{x}+be^{-x}+csin(x))}{xsin^2(x)}$
Forming linear equations by Taylor u get a+b=0,2a+c=0,(a/6-b/6-c/6)=2/3
So, a/6+a/6+a/3=2/3 So, a=1,b=-1,c=-2
SirLancelotDuLac
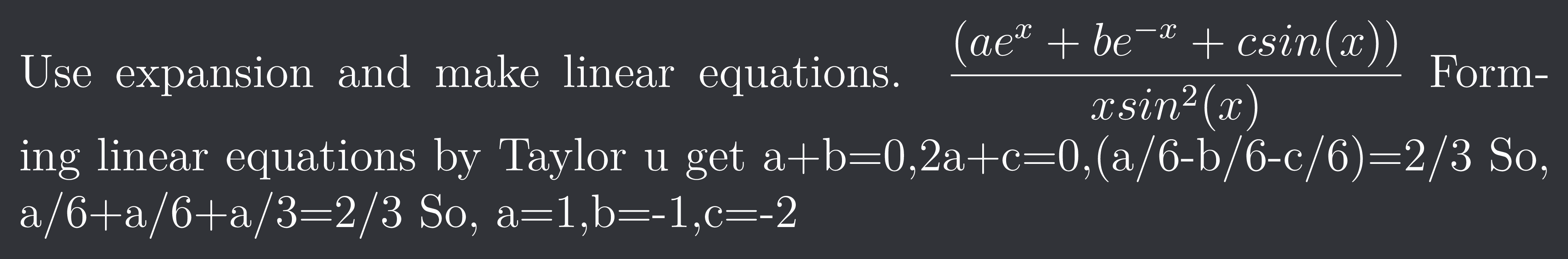
How did you get the third equation?
Equationg for x^3
x³? I don't understand
Basically the x^3 terms from the three expansions must sum up to 2/3x^3 for the limit to be equal to 2/3 (as denominator is also tending to x^3)
Oh the expansions.
I didn't do that at all mb.
l hopital would be recursive here.....if that was what you were applying?
I did what my teacher lovingly calls, "getting the numerator to commit suicide"
☠️
One round of L'Hôpital. That's it. But couldn't figure out anything after that
oh-
I usually don't go to L Hopital ngl.
Which is quite troublesome many-a-times
Got equation one from the given limit. Second equation from L'Hôpital round one. But any more doesn't help.
One round of differentiation is tolerable
yup at max 2
Not when you have a sin²x and product rule in the denominator
yup ☠️
3 eqns are made :
α+β=0
α-β-γ=4
α-β+γ=0
By equating with 0/0 form and series expansion of each e^x and e^-x and sinx...
But its not an indeterminant form so how are you applying series expansion
it is actually, notice the denominator approaches 0, and the limit exists finitely.....this leads us to a conclusion that the numerator must as well approach 0....
Ye I got it
+solved @Opt @Deleted User @Say_miracle_shadow
Post locked and archived successfully!
Archived by
<@1035556259417571408> (1035556259417571408)
Time
<t:1718990053:R>
Solved by
<@763645886500175892> (763645886500175892), <@1221329740959318107> (1221329740959318107), <@1245771182104510557> (1245771182104510557)