ITF
,tex \color{cyan} \sin ^{-1} \alpha+\sin ^{-1} \beta+\sin ^{-1} \gamma=\pi
Given
(\alpha+\beta+\gamma)(\alpha-\gamma+\beta)=3 \alpha \beta
\
Then \gamma = ?
30 Replies
Ansh Agarwal
Compile Error! Click the :errors: reaction for more information.
(You may edit your message to recompile.)
@Apu
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.√3/2 by my reckoning
Yes , how?
Well, consider a special case to make it easy on yourself first. Take α = β = ν = √3/2
Then you get the sum of arcsine of all those to be 3π/3 = π.
Check the condition. It holds. There you go
The second case to check is taking one of them to be zero, but that's not required here.
This is basically hit and trial , is there any other way out
Using a long ass formula.
Do you know the formula ??
Maybe I could give it a try with that
it means a + b + G = pi when is it possible it is only possilbe when you take all angles root 3/2
Not really.
aree bc yeh latex kahan se aaya
invsin x + invsin y
π/4+π/4+π/2.
π/2+π/2+0
I will continue the hit and trial approach
Or will try using SOT
Ig usse COS(SING) AAJAYEGA
$$sin^{-1} x + sin^{-1} y = sin^{-1} [x\sqrt{(1 - y^2)} + y\sqrt{(1 - x^2)}]$$
Keshav
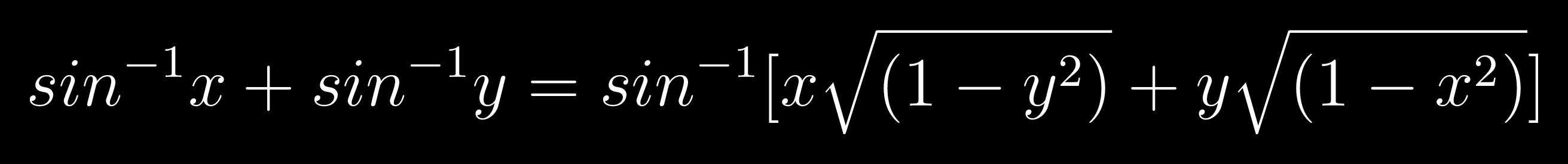
Thanks man
but iss se nhi hoga, bahut long jaayega
Yeah , ig in the exam we'll use @Opt ki approach, but for understanding ig ye sahi hai
$$(\alpha+\beta+\gamma)(\alpha-\gamma+\beta)=3 \alpha \beta$$
$$\alpha - \gamma =0$$
for $\beta$ to be a factor (Assuming, they are non-negative)
Keshav
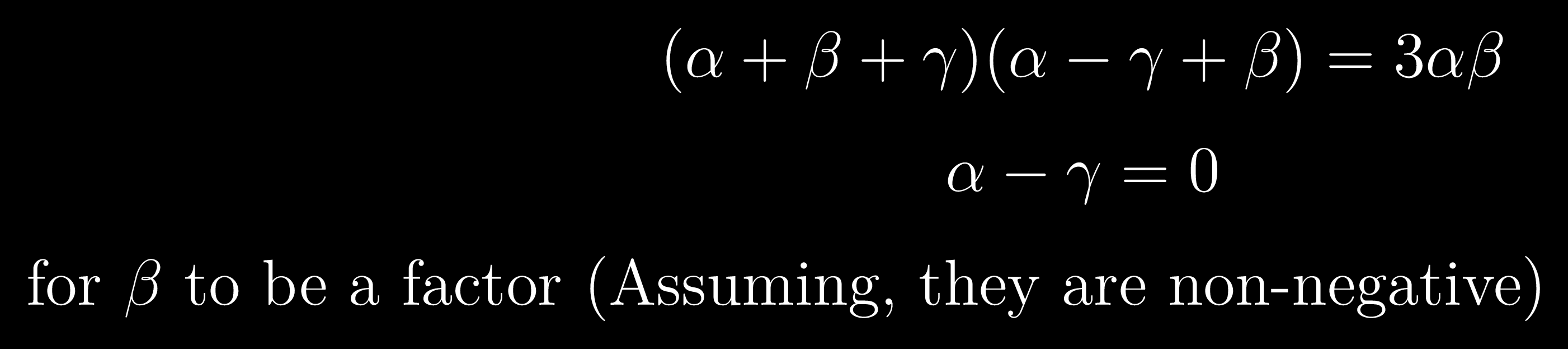
will this help
Definitely
yeah negative ho nhi sakte
Warna sum pi nhi hoga
so from here $\alpha = \gamma$
Keshav

but ab kaise findout karein ki alpha beta ke equal hoga ya nhi
,tex \color{red}
$\alpha = \beta??$
Keshav
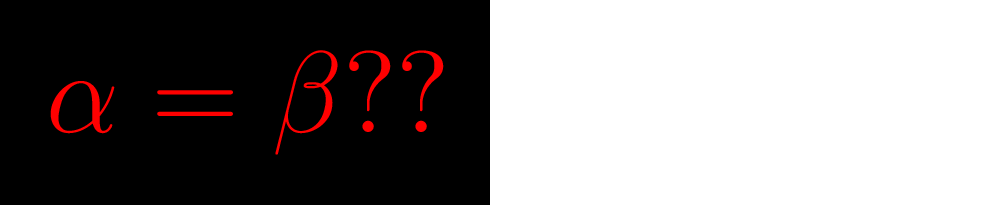
I just guess iske aage hit n trial ke alava koi option nahi
All the solutions I have come across are either using SOT or Hit N trial
I wanted a solution without those therefore tried asking here
Anyways thanks guys
+solved @Keshav @Opt
Post locked and archived successfully!
Archived by
<@783738581578940437> (783738581578940437)
Time
<t:1717774164:R>
Solved by
<@1082354613749035099> (1082354613749035099), <@763645886500175892> (763645886500175892)