Rotation
$$[\frac{1}{2} M (R/2)^2 + MR^2] \frac{\omega}{n}$$
Why can't I write $\vec{L}$ for the smaller disc about the axis of bigger disc in this way?

25 Replies
Keshav
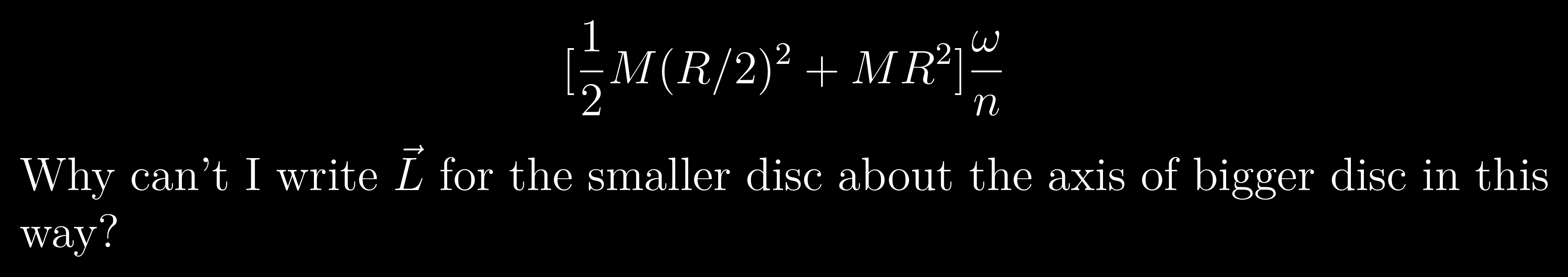
@Gyro Gearloose
Note for OP
+solved @user1 @user2... to close the thread when your doubt is solved. Mention the users who helped you solve the doubt. This will be added to their stats.Using Parallel axis theorem ^
the whole expression -->
Keshav
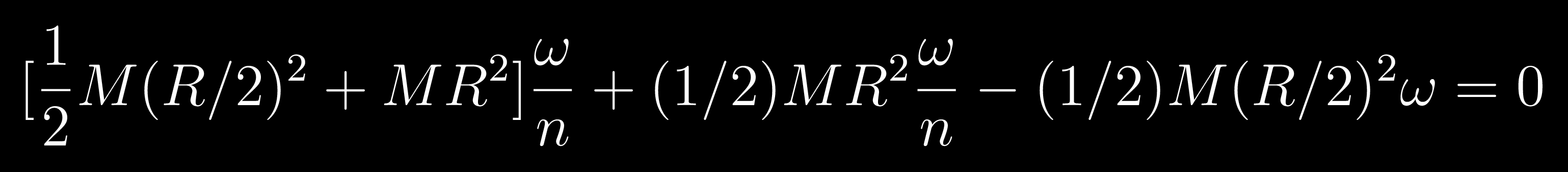
But from here we get n = 13 :/
Aisa lgta h College level physics likha h kuch
bruh
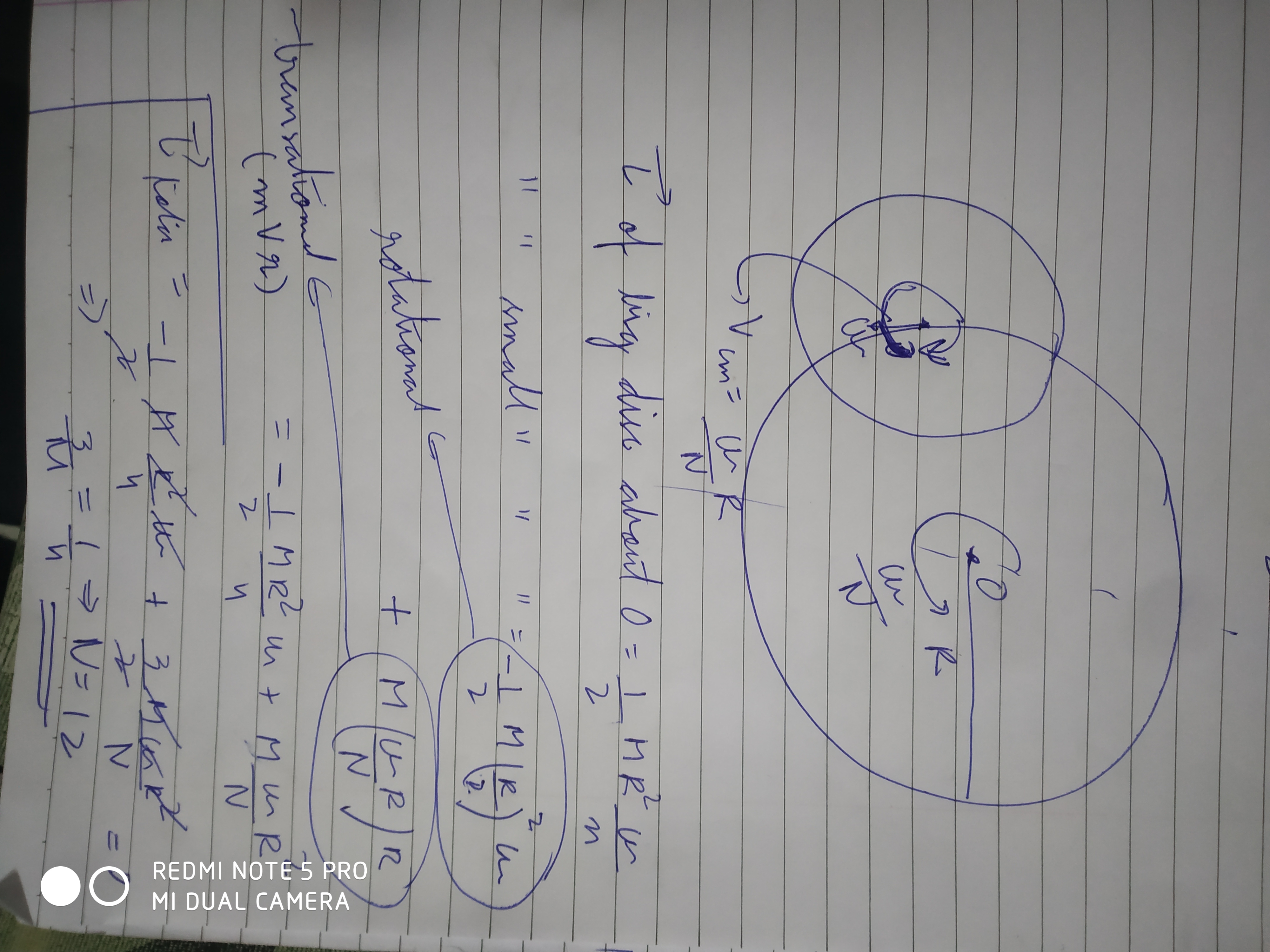
net MOI toh sahi hi nikala hai...
same shit here, yaha bhi MVcm*R se hi sahi answer aa rha, I net omega about hinge se nahi

but bhai
galti kahan ho rhi
haina bas 1 term ka difference hai
wahi toh
@Keshav VC aayega?
kidhar?
dms mein hi aaja
@Fermat's Last Theorem vc aaoge?
@Comrade Rock Astley
sorry nahi dekha
free rn?
Ha
toh keshav ka doubt dekh lo
Yo is this sorted?
@Keshav angular momentum about the rotational shaft should be conserved, because if you think about it to actually start the motion of the larger disc, some frictional torque would have been applied to actually start it in motion and until the system achieves a "steady state angular" velocity.....but if you start conserving A.M. about the axis of the larger disc, wouldnt it be wrong as now you got a frictional torque due to the generator shaft?
it is out of context but check out a question in S.S. Krotov (just for fun) about a smaller disc being kept on larger disc, and them achieving a steady state angular velocity.
+solved @lmaodedXD @Deleted User
Post locked and archived successfully!
Archived by
<@1035556259417571408> (1035556259417571408)
Time
<t:1719632400:R>
Solved by
<@1034231350141653132> (1034231350141653132), <@1221329740959318107> (1221329740959318107)