17 Replies
@Gyro Gearloose
Note for OP
+solved @user to close the thread when your doubt is solved. Mention the user who helped you solve the doubt. This will be added to their stats.Kq/x²
By my reckoning.
as x>>>>>R, R/x => 0
so yes, it'll be kQ/x²
$$x>>>>R$$
$$(x+R) \approx x$$
$$\frac{kQx}{(x^2+R^2)^{3/2}} \approx \frac{KQx}{x^3}$$
$$ \frac{kQ}{x^2}$$
Keshav
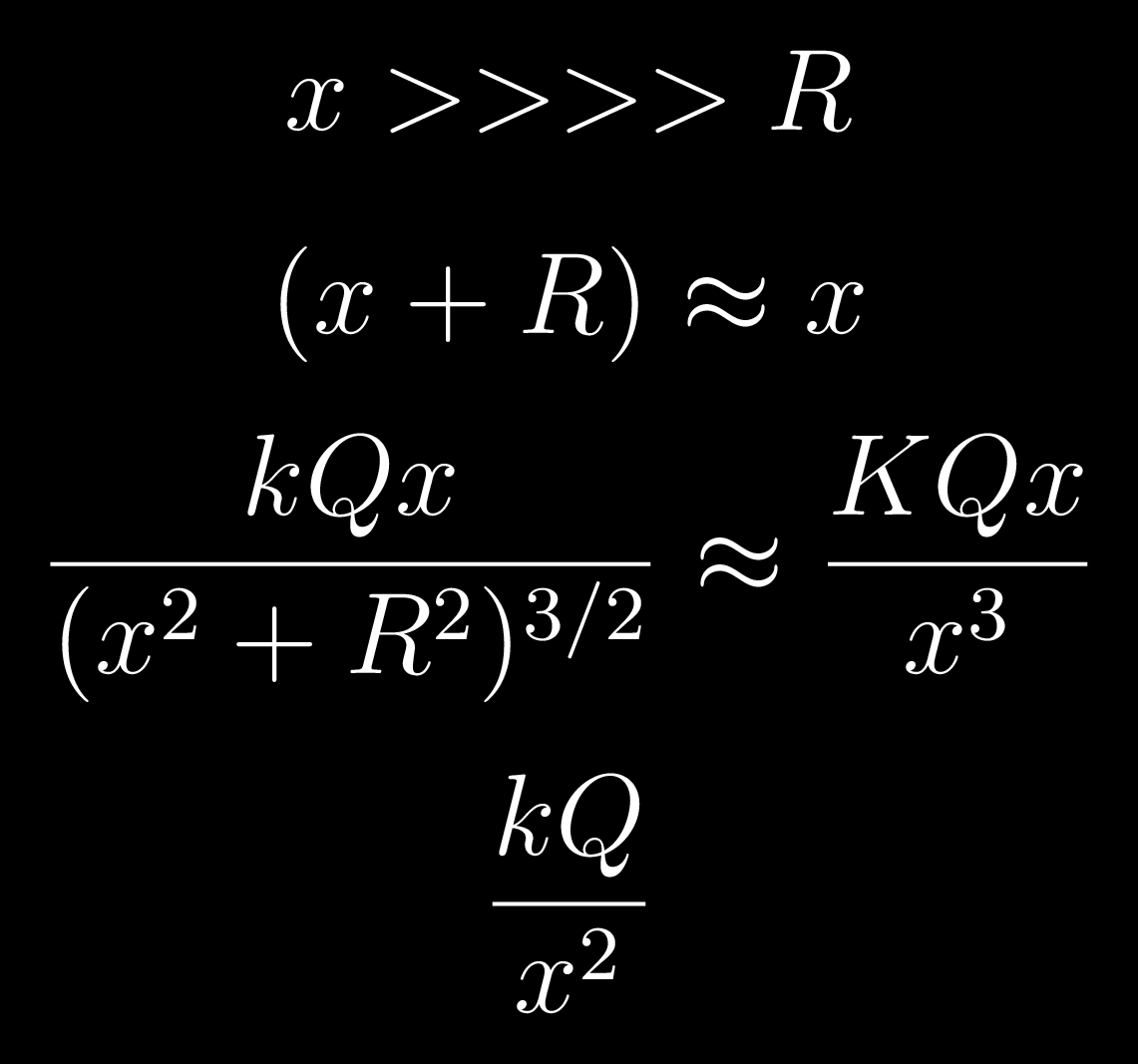
This is used a lot in Gravitation as well
Can you tell me what mistake did I do?
sir gave this question in binomial approximation
you didn't ignore that 3R^2 term
$$\frac{2kQ}{2x^2 + 3R^2}$$
$$since, x>>>R$$
$$2x^2 + 3R^2 \approx 2x^2$$
Keshav
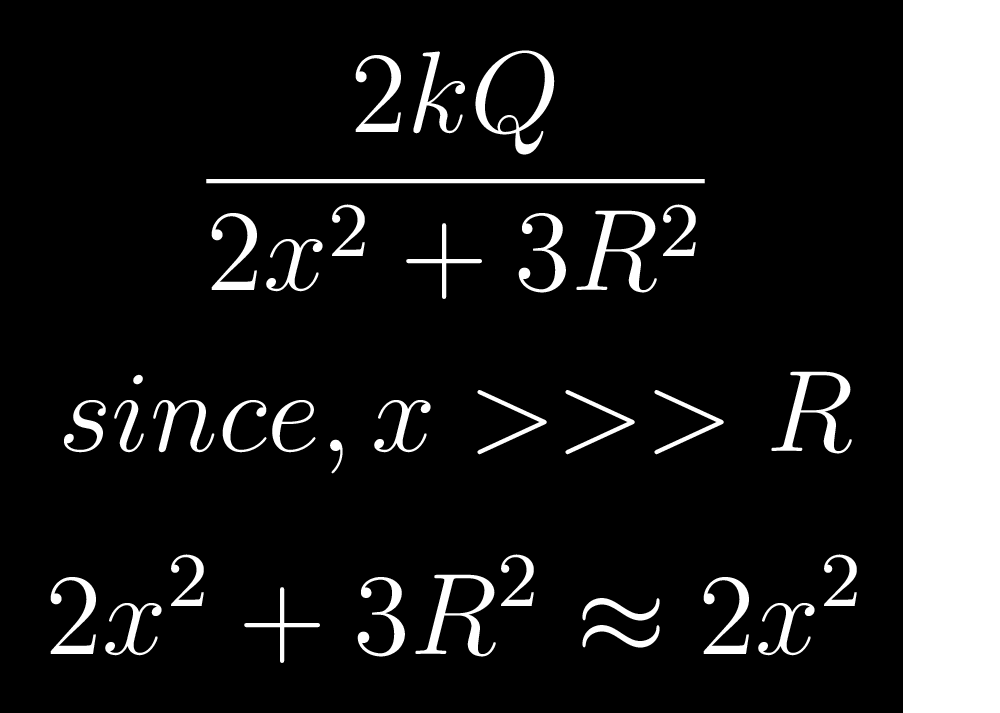
but mene to 1 + nx use kiya
@Keshav
wdym?
mene pehle (x^2 + R^2)^3/2 ko separately solve kiya using binomial approximation
check my solution
I think it should be
[KQ(x-3/2R)]/R^3
x >>>>R
Therefore
R²/x² ---> 0
U don't need binomial approximation for such small number u can just neglect it
The answer should be kQ/x²
oh okay then thanks
+solved @! SKULLxCRUSHER ]
Post locked and archived successfully!
Archived by
<@1179817028106858538> (1179817028106858538)
Time
<t:1717639758:R>
Solved by
<@742254253975928882> (742254253975928882)
