39 Replies
@Gyro Gearloose
Note for OP
+solved @user to close the thread when your doubt is solved. Mention the user who helped you solve the doubt. This will be added to their stats.$$\nabla \cdot \vec{E} = \frac{\rho}{\epsilon_{0}}$$
Oh that's an amazing one
Keshav
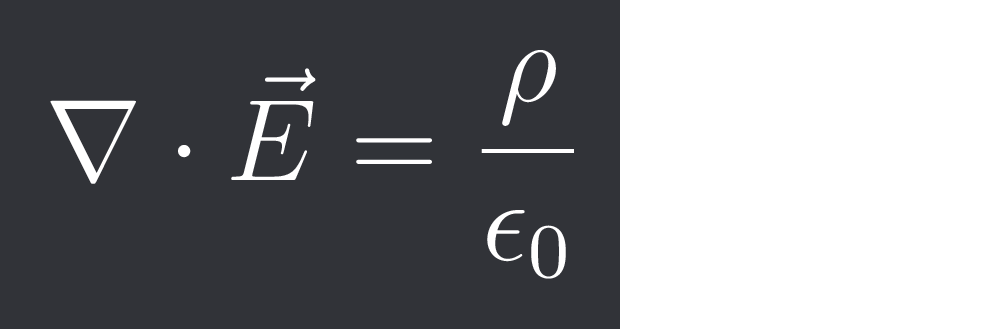
how to use this
Just a sec writing it down
btw they have missed something
$$\vec{E} = \frac{a(x\hat{i}+y\hat{j})}{x^2+y^2}$$
Keshav
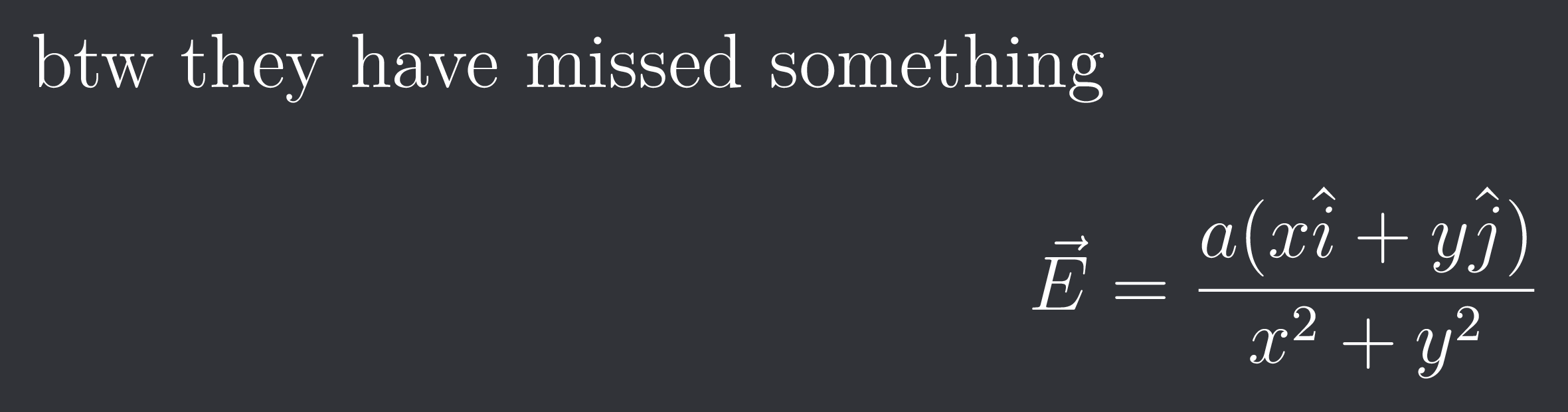
this is the given expression
ohk
Oh there's an a
that won't change a lot of things
Wait, is it necessary to use differential form? I'm using integral form rn. Just a sec
uh, ik how to solve this using integral form
but was curious if we can use differential form as we have the expression for Electric field
@Opt
Hmm I'm having trouble with the final integral
What did you get divergence of E to be?
$$div\cdot\vec{E}= \frac{\partial E{x}}{\partial x} + \frac{\partial E{y}}{\partial y}$$
Keshav
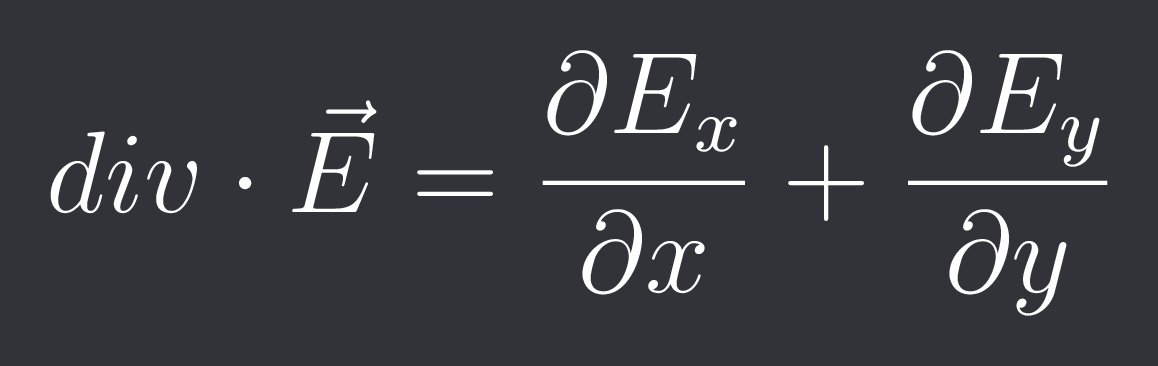
bhai @Opt div 0 aa rha 💀
check kr toh
Not this. I mean the final value.
Haan because origin pe infinite charge banega
so this doesn't works
@Opt so is it impossible to use this equation?
Mostly
Divergence is infinite at origin.
$$\frac{4}{x^2+y^2}$$
Opt
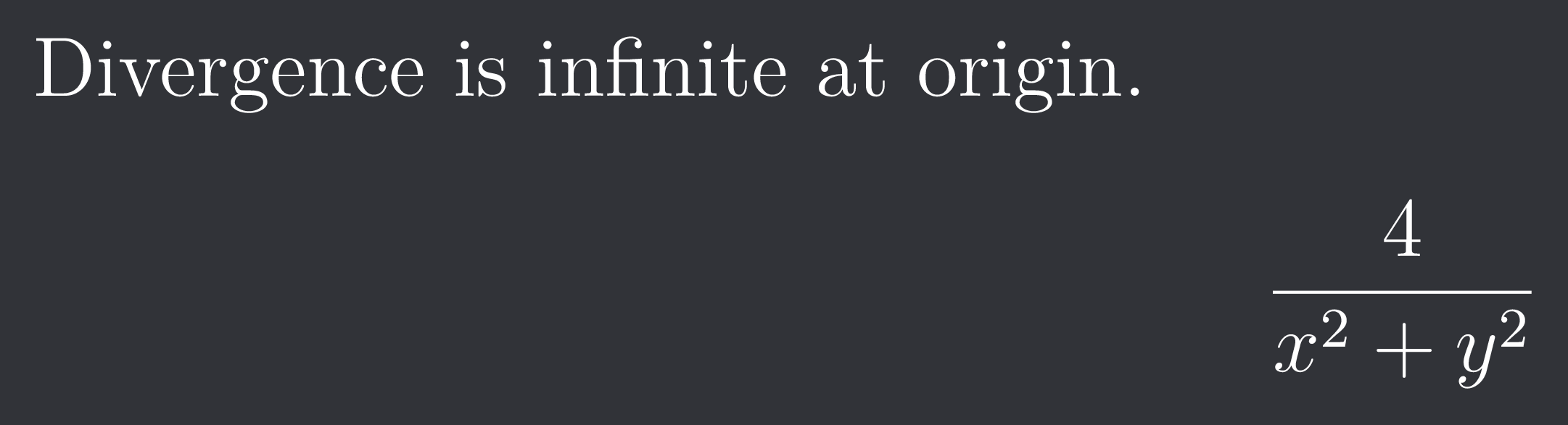
4/x^2+y^2??
Yup
Wahi toh aata hai differentiation karne par, right?
mera result 0 aa rha tha
$$\nabla$$
Ok I haven't used LaTex before. Need to learn.
Opt

Anyways, zero nahi aata
Varying with distance from origin. No chance the divergence is zero.
Distance from z-axis sorry
ok so if you result is correct what next?
$$\rho = \frac{Q}{4\pi a^2}$$
Keshav

Nope. That's wrong
oh yeah
You have to integrate on the volume. Directly substituting is impossible.
its making it harder lol
ig this equation is just making things harder for us
Yeah integral form is probably best here
Because origin is out of the equation if you only consider surface integral
yup
No zeroes in denominator.
+solved @Opt
Post locked and archived successfully!
Archived by
<@1082354613749035099> (1082354613749035099)
Time
<t:1717313299:R>
Solved by
<@763645886500175892> (763645886500175892)
